Sisteme informatice în tehnici de optimizare

instrucţiuni metodice
privind punerea în aplicare a instruirii practice

Disciplina - „Metode de optimizare“

Specialități - 230,700.62 „Informatică Aplicată“, 231,000.62 „Software Engineering“, 230,400.62 „Sisteme de informare și Tehnologii“, 080801 „Informatică Aplicată (în economie),“ 230105 „Software-ul de facilități informatice și sisteme automatizate“, 230,100.62 „Informatică și Inginerie“

Aprobat VPO „Universitatea de Stat-UNPK“ pentru a fi utilizate în procesul educațional ca linii directoare pentru învățământul profesional superior

Referent: Ph.D. Profesor asociat, Departamentul de IS O. V. Konyuhova

metodice conțin o descriere a celor cinci ateliere de lucru pe tema „Metode de optimizare“. Acestea sunt dedicate dezvoltării abilităților studenților în dezvoltarea modelelor matematice ale proceselor și informațiilor în zona de subiect; precum și să contribuie la dobândirea de competențe de cercetare experimentală în selectarea metodei de optimizare, ca și în rezolvarea problemelor tipice de optimizare. Instrucțiunile conțin informații teoretice cu privire la aspectele, exemple practice și informații de bază necesare pentru munca de laborator.

Liniile directoare sunt destinate pentru studenții full-time de specialitate 230700.62 „Informatică Aplicată“, 231,000.62 „Software Engineering“, 230,400.62 „Sisteme de informare și Tehnologii“, 080801 „Informatică Aplicată (în economie),“ 230105 „Software-ul de facilități informatice și sisteme automatizate“ 230,100.62 "Computer Science and Engineering".

Universitatea Tehnică de Stat Orel

Semnat la formatul de imprimare de 60 84 1 \ 16

Tipar off-set. Cond. Pec. l.5,6. Circulația 10 exemplare.

Imprimate cu un aspect original, finit

imprimarea pe baza „Universitatea de Stat VPO - ESPC»

Programarea 1.Lineynoe: simplex - Metoda 4

2.Spetsialnye problemă de programare liniară 19

3. Decizia de probleme întregi 23

4. Rezolvarea problemelor multiple criterii de optimizare 27

5. model de rețea, calculul principalilor parametri ai programului de rețea 31

Lecții practice №1

Programarea liniară: Metoda simplex pentru rezolvarea problemelor de programare liniară, probleme de interpretare geometrice

№2 lecție practică

Lecții practice №3

O decizie cu privire la probleme de optimizare neliniare. metoda multiplicatorului Lagrange.

Lecții practice №4

model de rețea, calculul principalilor parametri ai programului de rețea.

Construirea unui program de rețea

diagrame de rețea sunt direcționate grafice, arce, sau vârfurile care sunt atribuite unor valori numerice.

De obicei, în partea de sus, numit evenimentele corespund timpilor la începutul sau la sfârșitul uneia sau mai multor tranzacții și arc - operațiuni.

Există trei tipuri de evenimente: inițiale, intermediare și de închidere. Original - este un eveniment care începe executarea operațiunilor complexe. Închiderea corespunde obiectivului final, adică. E. Finalizarea tranzacțiilor complexe. diagrame de rețea cu un eveniment final câteva numit multifuncțional. Pentru intermediar include toate celelalte evenimente.

Evenimentele sunt, în general, notate cu cercuri. Se presupune că evenimentele nu au o durată de timp.

Momentul evenimentului împlinirii este considerată a fi sfârșitul performanței tuturor membrilor în caz de operațiuni. Până la toți membrii operațiunilor de eveniment nu se poate întâmpla evenimentul în sine, și, prin urmare, nu poate fi pornit, nici unul dintre ei imediat după operație.

Există trei tipuri de operațiuni:

1) exploatarea efectivă () - un proces care necesită timp și resurse (formulare Livrare de materiale, instalare de lucru etc.) ..

2) operațiune - așteptare () - un proces care necesită mult timp numai (intarirea betonului, uscare naturală ipsos înainte de începerea operațiunilor pictura, creșterea plantelor, etc.) ..

3) o operațiune de fals (), sau o dependență logică reflectă o resursă tehnologică sau de dependență în efectuarea anumitor operațiuni.

În construirea graficelor de rețea trebuie să respecte anumite reguli:

1) în rețeaua ar trebui să fie nici un eveniment (altele decât originalul), care nu este inclusă în nici un arc;

2) nu trebuie să fie evenimente (cu excepția finalei), din care nu depășește oricare dintre arc;

3) Rețeaua trebuie să nu conțină bucle;

4) orice pereche de programul de rețea de evenimente pot fi conectate la nu mai mult de un arc. Dacă reprezentăm efectuează simultan trei operații diferite. . cu pornire comun și evenimentele finale (Fig. 4.1), atunci confuzia apare din faptul că diferitele operații sunt aceleași notații (2.5). În acest caz, se recomandă să se introducă alte evenimente și să le conecteze cu următoarele operațiuni fictive (Figura 4.2.);

5) numărul de evenimente inițiale de orice operațiune trebuie să fie mai mic decât numărul evenimentului final.

Pentru a reflecta dependențele tehnologice sau de resurse în operațiile utilizate de operare dummy performante. Să presupunem că operația poate fi efectuată după finalizarea operațiunilor și. funcționare și - numai după ce operația este completă.

Această dependență este prezentată în Fig. 4.3, ceea ce arată că operațiunea în urma operației și operațiunea dummy (2, B).

Analiza datelor prezentate în acest tabel, secvența de lucru și interdependenței permite să construiască graficul de rețea prezentat în Fig. 4.4.

Sisteme informatice în tehnici de optimizare

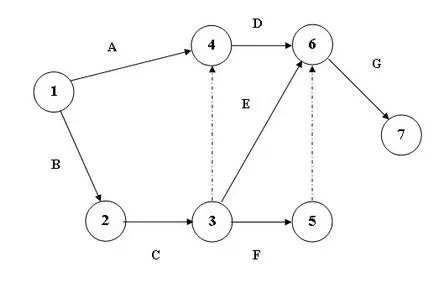
În plus față de această lucrare program de rețea specificată în tabel, două muncă dummy au fost utilizate (3.4) și (5.6), indicate prin linii punctate. Aceste lucrări nu au nevoie de timp pentru executarea lor și sunt folosite într-o reprezentare grafică a proiectului numai în scopul de a afișa în mod corect relația dintre lucrările.

Lecții practice №5

O ramură a matematicii care studiază situațiile de conflict pe baza modelelor matematice, numit teoria jocurilor. Se poate spune, de asemenea, că teoria jocurilor - teoria matematică a situațiilor de conflict, pentru a elabora recomandări privind cursul cel mai rațional de acțiune a fiecăruia dintre participanții la conflict, și anume, astfel de acțiuni, care să-l cel mai bun rezultat posibil, să furnizeze.

scheme de joc pot fi aplicate în multe situații economice. Câștig poate acționa astfel ca marja de profit, costul, eficiența utilizării resurselor limitate, instalațiilor de producție, etc.

Faptul esențial este că metodele și orientările dezvoltate teoria jocurilor așa cum se aplică unor astfel de situații de conflict, care au proprietatea de recurență multiple. În cazul în care o situație de conflict are loc o dată sau de un număr limitat de ori, recomandările teoriei jocului sunt ineficiente.

Analiza situației actuale de conflict necesită în mod semnificativ (uneori radicală) pentru a simplifica - luând în considerare numai factorii cei mai semnificativi pentru conflict. În acest sens, putem considera jocul ca un model matematic simplificat al situației de conflict, caracterizată prin prezența anumitor reguli. Aceste reguli:

1. Alegerea imaginii de acțiuni de jucători la fiecare etapă a jocului;

2. Informațiile pe care fiecare jucător are la realizarea unor astfel de alegeri;

3. Taxa pentru fiecare jucător, după finalizarea oricărei faze a jocului.

Strategia de joc este un set de reguli care definesc comportamentul jucatorului pe tot parcursul jocului. Strategia de fiecare jucător este rezultatele determinate sau a unei plăți în joc; și fiecare jucător are un set (finit sau infinit) de strategii posibile.

Printre caracteristicile definitorii ale jocului includ următoarele:

1. există părți implicate în conflict (jucători), factorii de decizie, ale căror interese nu coincid;

2. să formuleze strategii de selecție norme admisibile jucători cunoscuți;

3 definește un set de stări posibile ale jocului (de exemplu, câștig, pierdere, remiză);

4. toți participanții la joc (jucătorii) sunt cunoscuți în plăți în avans corespunzătoare fiecărei posibile stări finale.

situațiile de conflict întâlnite în practică, dau naștere la diferite tipuri de jocuri. Clasificarea jocuri disponibile pe diferite motive.

A) În funcție de numărul de jucători. Jocul poate lua parte orice număr finit de jucători. În cazul în care doar doi jucători, sau jucătorii sunt combinate în două grupuri care urmăresc obiective contradictorii, apoi la dublu. În funcție de numărul de politici în joc, acestea sunt împărțite în finit și infinit.

B) În funcție de relațiile dintre participanți se facă distincția între jocuri non-cooperative (participanții nu au dreptul de a încheia un acord), și de cooperare (uneori sinonime - jocuri non-cooperative și de cooperare, respectiv).

B) În funcție de natura câștigă jocul sunt împărțite în joc cu sumă zero, și non-zero sumă. Într-un joc cu sumă zero, capitalul total al jucătorilor nu se schimba, dar numai redistribuit în joc, și, prin urmare, valoarea câștigurilor este egală cu zero (în acest caz, pierderea este văzută ca un câștig negativ). În jocurile cu o sumă nenulă din valoarea câștigului este diferit de zero.

D) În funcție de tipul de jocuri funcțiile payoff sunt împărțite în matrice, bimatrix etc. Jocurile de matrice (pentru două persoane) câștigă primul set de matrice jucător în bimatrix. - câștigă fiecare jucător sunt definite prin matricea sa.

D) din numărul de rotații ale jocului sunt împărțite într-un singur sens (câștiga distribuite după unul din fiecare jucător) și multitrecere (câștigurile distribuite după mai multe accidente vasculare cerebrale).

strategia unui jucător se numește optimă dacă acesta oferă acest jucător sub joc repetat cel mai mare câștig mediu posibil sau cea mai mică pierdere medie posibil, indiferent de comportamentul inamicului.

În viitor, ne vom limita la perechea de matrice de jocuri cu sumă zero. Stabilirea unor strategii ale celor doi jucători în joc dublu de acest tip determină complet rezultatul, și anume castiga sau pierde unul pe altul. După cum sa menționat deja, perechea finală de joc cu sumă zero poate seta matricea, rândurile și coloanele care corespund diferitelor strategii pentru 1 și jucătorii 2, respectiv, și elementele sale - câștigurile pe de o parte (în alte înregistrări egale pierderi). Această matrice se numește o matrice payoff sau jocuri de matrice.

Jocuri fără puncte de șa

Deci, în cazul în care matricea de joc cuprinde un punct de șa, este o decizie pe principiul minimax. Luați în considerare metoda de rezolvare a jocului în matricea de plată care nu are un punct de șa. Strategiile de minimax Aplicarea fiecare jucător oferă un prim câștig mai puțin. și a doua pierdere nu mai. Având în vedere că. în mod natural pentru jucătorul vreau să crească câștigul, iar jucătorul II - pentru a reduce pierderile. Căutarea unor astfel de soluții conduce la utilizarea unei strategii complexe, care constă într-o utilizare aleatorie a două sau mai multe strategii pure cu anumite probabilități. O astfel de strategie complexă în teoria jocurilor se numește mixte. Strategiile mixte de jucători I și II vor fi notate, respectiv,

în cazul în care. # 8209; probabilitatea strategiilor pure corespunzătoare. Evident, în cazul în care condiția de normalizare pentru probabilitatea

Una dintre teoremele fundamentale ale teoriei jocului afirmă că fiecare joc finit de două persoane zero sumă are cel puțin o soluție poate fi în strategii mixte. Aceasta teorema implică faptul că fiecare joc finit are un preț. Am precum și valoarea netă a jocului prin denote. Prețul de joc - câștigul mediu pe o parte - întotdeauna satisface. și anume Aceasta se află între () inferior și superior () prețurile de joc. Prin urmare, fiecare jucător sub jocuri repetate, lipirea la strategii mixte, primește un rezultat mai favorabil pentru ei înșiși. Soluția optimă a jocului în strategiile mixte, precum și o soluție în strategii pure, caracterizată prin faptul că fiecare dintre jucătorii care nu sunt interesați să se mute departe de strategia optimă mixt în cazul în care adversarul său se aplică strategia optimă mixtă, așa cum este în avantajul său.

Strategii de jucători în cadrul strategiilor lor mixte optime se numesc activi.

5.5 Utilizarea de optimizare liniară pentru rezolvarea jocurilor matriceale

Să jocul nu este cea mai bună soluție în strategiile pure, adică punctul șa lipsește.

Presupunem că toate elementele matricei de plată non-negativ (în cazul în care nu este, este posibil să se toate elementele matricei pentru a adăuga un număr de L, trimiterea de plăți la valori non-negative - în mod evident, prețul jocului va crește la L, iar decizia nu se va schimba problema). Astfel, presupunem că> 0.

Noi căutăm soluția de joc în strategiile mixte

Utilizarea de jucător I strategia optima mixt il asigura, indiferent de comportamentul jucatorului II, câștigul nu este mai mic decât prețul de joc.

Lăsați jucătorul II utilizează strategia puternică netă j-a, iar jucătorul I - strategia lor optimă. Apoi, jucătorul medie I câștig va fi egal

Având în vedere că nu poate fi mai mică. scrie condițiile:

Împărțind ambele părți ale fiecăreia dintre inegalitățile (5.4) cu privire la prețul de joc. obținem

Când se utilizează simboluri

(5.5) ia forma

în cazul în care aparent totul. din moment ce.

și definiția (5.6) rezultă că variabilele () satisfac condiția

Având în vedere că jucătorul I urmărește să maximizeze. Obținem o funcție liniară

Astfel, problema se reduce la rezolvarea joc urmatoarea problema de optimizare liniara: găsi o valori variabile non-negative, minimizând o funcție liniară (5.8) și care îndeplinesc constrângerile (5.7).

Prin rezolvarea problemei de optimizare liniara este ușor de a găsi valoarea jocului și strategia optimă pentru jucătorului I:

La rândul său, strategia optimă pentru jucător al II-lea

Acesta poate fi găsit din expresia

în cazul în care - variabile non-negativ problemă de optimizare liniară

care este dublu față de problema prezentată de condițiile (5.7) și (5.8).

În acest sistem de variabile inegalitati

Astfel, strategia optimă

jocuri cu matricea de plată () poate fi găsită prin rezolvarea perechii simetrice a duale probleme de optimizare liniară.

Problema dublă problemă inițială

Prețul de joc, și probabilitatea de strategii de jucător I și II sunt

5.6 Sarcini pentru decizia independentă

Prin reducerea problemelor duale de programare liniară pentru a găsi strategia mixtă optimă și prețul de jocuri matrice jocuri cu o astfel de matrice payoff: