Setul de numere reale

În cazul în care setul de numere raționale pentru a completa setul de numere iraționale, apoi împreună constituie setul de numere reale. Setul de numere reale este de obicei notată cu litera R; folosit, de asemenea, notație simbolică (-∞, + ∞) sau (-∞, ∞).

Set de numere reale pot fi descrise ca un set de zecimale finite și infinite; rămase în urmă zecimale și fracții zecimale periodice infinite - numere raționale, și fracții zecimale infinite neperiodice - numere iraționale.

Fiecare număr real poate fi reprezentat printr-un punct de pe axa de coordonate. Pe de altă parte, fiecare punct are un valabil de coordonate axe de coordonate. Matematică spun de obicei: R între mulțimea numerelor reale și o multitudine de puncte set de coordonate reciproc axa one corespondență. Axe de coordonate este un model geometric al setului de numere reale; Din acest motiv, axa de coordonate folosesc adesea linia reală pe termen lung.

Notă: coordonatei axa pe care s-au bucurat din clasa a 5-a. Dar, se pare, cunoștințele dumneavoastră a fost un decalaj de justificată: nu pentru orice axă de coordonate, au reușit să găsească o coordonată - doar un profesor vă protejează de acest necaz.

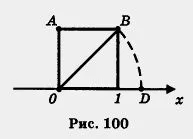
Să considerăm un exemplu. Dana coordona linie, interval unitate pătrat sa construit (Fig. 100), diagonala pătratului RH amânat pentru a coordona o linie dreaptă de la punctul O la dreapta, am obține punctul D. Care este coordonatele punctului D? Acesta este egal cu lungimea diagonalei pătratului. t. e .. Acest număr, după cum știm acum, nu este un număr întreg sau fracțiune. Deci, nici în a 5-a sau a 6-a sau a 7-lea grad de coordonate punctul D, nu te-ai putut găsi.

Pentru că suntem încă, și a spus, „linia de coordonate“ mai degrabă decât „linia reală“.

Rețineți că a existat un alt decalaj justificabil cunoștințele de algebră. Luând în considerare expresiile cu variabile, am presupus întotdeauna că variabilele pot lua orice valori valide, dar numai rațională, pentru că celălalt-nu a fost. De fapt, variabile pot lua orice valori valide reale. De exemplu, în identitatea (a + b)

Pentru numere reale a, b, c sunt realizate legi uzuale.

a + (b + c) = (a + b) + c

(A + b) c = ac + bc și t. D.

Realizarea si regulile uzuale: produsul (câtul) a două numere pozitive - un număr pozitiv;
produs (câtul) a două numere negative - un număr pozitiv; produs numărul (privat) de pozitive și negative - număr negativ.

Numerele reale pot fi comparate unele cu altele, folosind următoarea definiție.

Definiția. Se spune că numărul real și mai mari (mai mici), numărul real b, în cazul în care diferența lor a - b - un număr pozitiv (negativ). Scrieți un> b (o

Această definiție implică faptul că orice întreg pozitiv și este mai mare decât zero (ca diferența A - 0 = a - un număr pozitiv) și fiecare număr negativ b este mai mică decât zero (ca diferență b - b = 0 - negativ).

Deci, un> 0 înseamnă că - un număr pozitiv;

și <0 означает, что а — отрицательное число;
a> b înseamnă că un -b - un număr pozitiv, adică a - b> 0 ..;
oși anume și - b <0.

Împreună cu semne de inegalități stricte (<,>) Utilizați semne inegalități stricte:

în timp ce 0 înseamnă că o mai mare decât zero sau egală cu zero, adică - un număr întreg non-negativ (pozitiv sau 0), sau nu mai puțin de zero ..;

în timp ce 0 înseamnă că o mai mică decât zero sau egal cu zero, adică - o valoare non-pozitiv (negativ sau 0), sau că nu este mai mare decât zero ..;

și b înseamnă că o mai mare sau egal cu b, adică a - b - un număr non-negativ, sau care nu este mai mică decât b ..; și - b 0;

și b înseamnă că este mai mic sau egal cu b, adică a - b - numărul nonpozitiv, sau nu mai mare de b ..; și - b 0.
De exemplu, pentru orice număr și inegalitate 0 și 2;

pentru orice numere a și b, inegalitatea (a - b) 2 0.
Cu toate acestea, pentru compararea numerelor reale de fiecare dată să fie opțional, diferența lor și pentru a afla, este pozitiv sau negativ. Acesta poate fi învățate prin compararea numărului de înregistrare ca o fracție zecimală.

.. Modelul geometric al setului de numere reale, și anume, linia numărul, face ca numarul de comparare de funcționare deosebit de evidente: două numere a, b mai mult decât cea care se află pe linia de număr la dreapta.

Astfel, în comparație cu numerele reale trebuie să fie abordată destul de flexibil, pe care le folosim în acest exemplu.

Exemplul 1: Comparați numărul de:

Exemplul 2. Aranjați în ordinea crescătoare a numărului de

Planificarea materialelor de matematica din clasa de matematică 8 descărcare. manuale on-line

Dacă aveți corecturi sau sugestii la această lecție, vă rugăm să ne contactați.

Dacă doriți să vedeți alte ajustări și sugestii pentru lecții, uita-te aici - Forumul Educațional.