Segmentul care conectează centrul cercului cu orice punct de aceeași - prezentare 15733-4

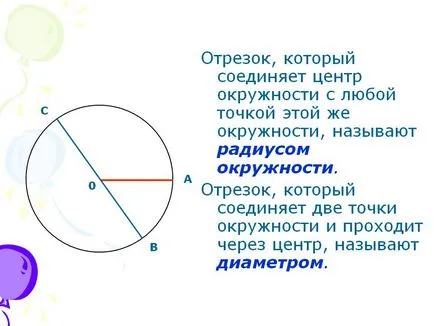
Segmentul care conectează centrul cercului cu orice punct al cercului se numește raza cercului. Segmentul care face legătura între două puncte ale cercului și trece prin centrul, numit diametrul.

Slide 4 al prezentării „cercului și cercul«la lecția de geometrie pe»Cercul"

Dimensiuni: 960 x 720 pixeli, format: jpg. Pentru a descărca diapozitivul pentru a fi utilizat pe o lecție de geometrie, faceți clic pe dreapta imaginii pe butonul mouse-ului și faceți clic pe „Save Image As. “. Descărcați întreaga prezentare a „Cercul și krug.ppt“ poate fi în dimensiunea-zip arhiva de 231 KB.

cerc

„Cerc Inscripționată“ - cerc înscris. Date fiind: AB, AC - tangente, punctele B, C unghiului tangență BAC = 56 °, OS = 4 cm dascăl Saynakova Rasim Sayfullovna matematică noiembrie Zyryanskaya SOSH № 2. Căutare: Unghi CCA RH .. Dovedește: O, punctul de intersecție al Bisectoarele ABC ?. Teorema: cerc poate fi înscris în orice triunghi. EFMN circumscris în jurul unui cerc descris DKMN nu este vorba despre un cerc.

„Tangentă la cercul» - tangenta M. Proprietatea. Punctul de atingere. Un semn al tangenta. Să d - distanța de la centrul O la linia KM. segmente O. AK și AM segmente numite tangente trasate de la A. Atunci. Tangent.

„Cercul circumscrisă“ - care este echidistant față de centrul triunghiului înscris într-un cerc? Centriștii. Poligon - înscris. Ceea ce este descris de un cerc? poligon Inscripționată. Triunghiurile și cercuri. Ce este un arc? Triunghiuri Cum a apărut conceptul de cerc? Cum de a scrie \ vom descrie un cerc de fericire?

"Ellipse" - Ce este o elipsă. Craterele de pe Luna au, de asemenea, o formă eliptică. Elipsă. Să trecem creionul pe hârtie, astfel încât firul rămâne întins. Se pare că toate planetele se mișcă în jurul Soarelui nu este un cerc, ci o elipsă. Fixați capetele firului la trucuri. Punctul de ansamblu se numește punctul de contact. Tangent.

Doar un „cerc“ tema 21 Prezentare