Rezolvarea problemelor de programare liniară grafic

Definiția. Orice decizie prin sistemul de constrângeri se numește o soluție fezabilă ZLP.
Definiția. O soluție valabilă în care funcția obiectiv atinge o valoare maximă sau minimă se numește o soluție optimă.

Prin aceste definiții problemă LP poate fi formulată după cum urmează: la toate punctele regiunii convex, care este un sistem de constrângeri soluție pentru a selecta astfel de coordonate, care minimizează (maximizare) funcția F liniar = + s1x s2y.
Rețineți că variabila x. y în ZLP ia valori, de obicei, ne-negative (x ≥ 0, y ≥ 0), astfel încât regiunea se află în trimestrul I de coordonate plane.

Luați în considerare funcția F liniar = + s1x s2y și să fixeze o parte din valoarea sa F. Să presupunem, de exemplu, F = 0, adică, s1x ​​s2y + = 0. Graficul acestei ecuații este linia care trece prin origine (0, 0) (Fig.).
imagine
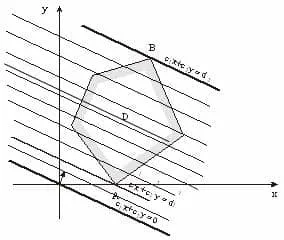
Modificarea acestei valori fixe F = d. s2y s1x drepte + = d va fi deplasat în „zachertit“ plan întreg paralel și. Fie D - poligon - o zonă aflată la soluții de sistem de limitare. La schimbarea d linia s1x s2y + = d. pentru o anumită valoare a d = d1 D. ajunge la acest punct se numește poligon un „punct de intrare“, și apoi, după ce trece un poligon, pentru o anumită valoare a = d d2 va avea cu el ultimul punct comun este numit V. În „punctul de ieșire.“
Este evident faptul că cele mai mici și cele mai mari valori ale funcției sale obiectiv F = + s1x s2y ajunge la punctele „de intrare“ A și „ieșire“ B.
Având în vedere că valoarea optimă pe setul de soluții fezabile funcției țintă ia la nodurile de D. poate propune următoarea decizie planului ZLP:

1. construi limitări suprafață ale soluțiilor;
2. construi o linie corespunzătoare funcției țintă și translație paralelă a acestei linii pentru a găsi un punct de „intrare“ sau „ieșire“ (în funcție de cerințele pentru a minimiza sau maximiza funcția obiectiv);
3. determină coordonatele acestui punct, ele se calculează o valoare a funcției obiectiv.

Rețineți că vectorul (c1. C2) perpendicular pe linia dreaptă care arată direcția de creștere a funcției obiectiv.

La o soluție grafică ZLP două cazuri posibile care necesită o atenție specială.

cazul 1

Figura 6
Atunci când se deplasează s1x drept s2y + = d «intrare“ sau «ieșire» (așa cum este arătat), are loc pe latura poligonului. Acest lucru se va întâmpla în cazul în poligon are laturi paralele cu linia + S1H s2u = d.
În acest caz, punctele de „ieșire“ ( „input“) nenumărate - și anume orice punct al segmentului AB. Acest lucru înseamnă că funcția țintă presupune valoarea maximă (minim) nu la un moment dat, și toate punctele culcat pe o parte respectiv a poligonului D.

cazul 2
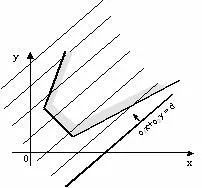
Luați în considerare în cazul în care intervalul de valori admise este nelimitat.
În cazul unei regiuni nelegata a funcției obiectiv poate fi definit astfel încât „ieșire“ (sau „intrare“), care corespunde nu are nici un punct direct. Apoi, valoarea maximă a (minim) nu este atins niciodată - spun că funcția nu este limitat.

imagine
Este necesar să se găsească valoarea maximă a funcției obiectiv F = 4x + 6Y → max. atunci când constrângerile sistemului
Noi construim o regiune fezabilă, și anume, rezolva grafic un sistem de inegalități. Pentru aceasta vom construi fiecare linie și definesc jumătate de planul definit de inegalitățile.
x + y = 18

Construi linia corespunzătoare valorii funcției F = 0. 4x + 6Y = 0. Vom trece linia într-un mod paralel. Dintre toate familiile liniilor 4x + 6y = const ultimul nod, prin care trec direct la ieșirea frontierei poligon va fi vârful C (12, 6). Este aici că F = 4x + 6Y atinge valoarea sa maximă.
Prin urmare, atunci când x = 12, y = 6, funcția F atinge valoarea sa maximă F = 4 # 8729; 12 + 6 # 8729; 6 = 84, egal cu 84. Punctul cu coordonatele (12, 6) satisface toate constrângerile sistemului inegalitățile și în ea valoarea funcției obiectiv optim F * = 84 (valoarea optimă va fi notată cu „*“).
Problema este rezolvată. Deci, este necesar să se elibereze 12 produse de tip I și de tip 6 produse II, cu un profit de 84 mii. Frecați.

Metoda grafică este utilizată pentru a rezolva problemele care au avut doar două variabile într-un sistem de constrângeri. Această metodă poate fi aplicată la sistemele de inegalități, cu trei variabile. Geometric, situația va fi diferită, rolul va fi jucat cu avionul directe în spațiul tridimensional, și soluția de inegalitatea dintre cele trei variabile vor fi o jumătate de spațiu, situat pe o parte a planului. Rolul regiunilor va juca un poliedru este intersecția de jumătate de spații.

Reguli de introducere a datelor

Puneți întrebări sau să facă sugestii sau comentarii pot fi partea de jos a paginii, în secțiunea Disqus.
Puteți trimite, de asemenea, o cerere de ajutor în a face cu examene de partenerii noștri de încredere (aici sau aici).