produse de conversie a funcțiilor trigonometrice în valoare de - Lecția

O scurtă descriere a documentului:

În ciuda faptului că trigonometria, știință, a existat destul de mult timp, aceasta nu și-a pierdut relevanța astăzi. În diferitele științe există probleme soluția pe care elevii trebuie să se ocupe de acest domeniu. Din acest motiv, acestea ar trebui să fie în măsură să se ocupe cu exemple de complexitate diferite, luați în considerare funcția care conține sinus, cosinus, tangenta și cotangentă etc.

Deoarece trigonometria conține un număr foarte mare de formule, fără de care simplificarea unei expresii ar lua o mare cantitate de timp. Prin urmare, este foarte important este amintindu-și de înțelegere a acestor formule. Dacă ați înțeles procesul de eliminare a acestora, vă puteți aminti cu ușurință și să aplice în practică. Pentru ca ei să rămână în memorie pentru o lungă perioadă de timp, trebuie să fie consolidate în practică. De aceea, profesorii trebuie să ceară de la casa unui număr mare de expresii trigonometrice și ecuații pentru elevi.

Copiii de școală știu deja cum este necesar pentru a converti suma ecuațiilor trigonometrice în produs. Cum se poate realiza un proces invers, dacă este necesar? Uneori, pentru simplificarea unei expresii va fi o necesitate.

Începe cu atenție la acestea. lucrări scrise ale unor TNA cosinus sine cu aceeași valoare. Transformă această expresie printr-o fracție, în care numărătorul este suma sinus vedem suma și diferența dintre argumentele divizate de 2.

De asemenea, produsul este convertit la sinusal unele s sinusul t.

Pentru a asigura practica de exprimare a datelor propuse pentru a rezolva câteva exemple. Primul dintre acestea se propune pentru a găsi răspunsul numeric pentru exprimare, care este un produs al sinusul și cosinusul 2x 9x. In rezolvarea acestui exemplu folosit formula anterior studiate. Ecranul afișează un exemplu detaliat al deciziei arată, de asemenea, ce fel de formulă este utilizat.

Al treilea exemplu oferă beg expresie, care constă din produsul de trei sinus unele valori grade. În simplificarea formulei este utilizată în produsul de conversie a sumei sine. În rezolvarea acestui exemplu evidențiază faptul că funcția cosinus este o funcție chiar. Astfel, semnele sunt determinate corect. răspuns de ieșire. Volumul de soluție este suficientă, dar dacă pas cu pas să-l ia în considerare, atunci nimic nu va fi lăsat necunoscut.

După cum sa menționat deja, cu ajutorul acestei prezentări poate fi făcută lecție interesantă pentru a zecea. Descarcă materialul poate tutori și studenți. Cu acesta, puteți afișa vizual pas cu pas soluție de student de exemple în care similitudinea dintre elevii vor veni peste ca in timpul teme, și de auto-control și munca la școală.

Conversiilor funcționează în suma expresiilor trigonometrice

Știi deja că orice formulă matematică utilizată în practică, de la dreapta la stânga și la stânga la dreapta. În consecință, aplicarea formulei în sens invers, putem lucra funcții trigonometrice pentru a converti la bani.

Conversia din formula sume de sinus și argumentele ec te în proizvedeniesin (s + t) + sin (s - t) = 2 pacate costa

puteți obține o altă formulă:

Păcatele costa = (produsul argumentului sinusoidale es TE argument cosinus este egală cu jumătate din suma sumei sinus a es argumente și te diferența sine și a es argumente și Te, iar diferența este considerată cea a argumentului stă sub semnul unghiului sinus scade în picioare pentru semnul cosinus. )

In mod similar, formula se ridică cosinus transformă argumentul și te ec în cos produs (i + t) + cos (s - t) = 2 costuri coss obțină

coss costul = (produsul din es argumentul cosinus și Te este egală cu jumătate din suma acestor argumente cosinus ale cosinusul și diferența lor).

Și din cosinusul diferenței formule de transformare ec și argumentele proizvedeniecos s + TE (t) - cos (s - t) = - 2sins au sint

Păcatele = sint (produs de sinus și argumente es te pe jumătate cosinus este egală cu diferența dintre aceste argumente cosinus și sumele acestora).

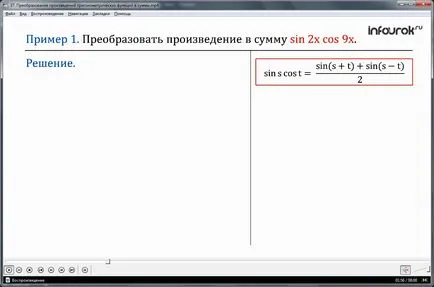
Exemplul 1. Se convertește produsul la cos9h sum sin2h.

Decizie. În cazul în care decizia va fi de a folosi formula păcatele cost =. unde s = 2, t = 9x. Apoi, putem scrie

sin2hcos 9x = (având în vedere că

sin (y) = -sinu obține) = (jumătății sine unsprezece X și sinus șapte X).

Raspuns: sin2h cos9h =.

EXEMPLUL 2: Se transformă produsul unei sume de cos (2x - y) cos (x + tip benchmark 4 ani) (produsul din cosinusul argumentului, cele două X minus y la cosinusul argumentului X plus patru y).

Decizie. În cazul în care decizia va fi de a folosi formula Coss = costul. unde s = (2-y), t = (x + 4y). atunci

cos (2x - y) cos (x +) = = tip benchmark 4 ani = dezvăluie bretele. vom efectua calcule și de a obține

= (Jumătate din suma cosinusul argumentului, trei plus trei X y și cosinusul argumentului X minus cinci y).

EXEMPLUL 3 Expresia simplificată sin20 ° sin40 ° sin80 °.

Decizie. Aplicăm formula: = păcate sint.

păcat 20 ° păcat 40 ° păcat 80 ° = sin ∙ 80 ° ∙ = sin 80 ° =

(Menționăm că cosinus - funcția este chiar, atunci

= ∙ păcat 80 ° Deoarece cos60 ° =

= ∙ păcat 80 ° = ∙) ∙ păcat 80 ° =

(Rețineți că păcatul 80 ° = sin (90 ° - 10 °) = cos10 °, prin urmare, că se obține)

= ∙) ∙ cos10 ° = = ∙ dezvăluie paranteze cos10 ° - ∙ cos10 °

(Aplicabil costul coss formula =)

Răspuns: sin20 ° sin40 ° sin80 ° =.

Exemplul 4. Rezolva ecuatia 2 sin2h cos9h - sin11h = 0.

Transformam partea stângă a ecuației cu ajutorul formulei

sin s cos t =. GDES = 2x, un t = 9x obține

2 ∙ - = sin11h sin11h =.

Deci, această ecuație este echivalentă cu ecuația = 0 (minus sine șapte X este zero). Deci, = πn, unde x =.