Poli și zerouri

Multe dintre proprietățile dinamice ale sistemului (de exemplu, viteza, supraoscilației) sunt determinate de polii funcției de transfer (sau, echivalent, valorile proprii ale matricei

Modelul în spațiul de stat).

Funcția de transfer poate fi scris ca produs al funcțiilor de transfer ale unităților elementare ale primului și al doilea ordin. Astfel, o pluralitate de poli ai funcției de transfer a unui sistem stabil constituie funcții de transfer pol ale celor două tipuri de unități elementare: aperiodice și oscilatorie.

link-ul aperiodic cu funcția de transfer a formularului

Ea are o caracteristică unică - constanta de timp

. De la aproximativ 5 frecvență

, Răspunsul în frecvență al legăturii începe să scadă, se apropie de zero.

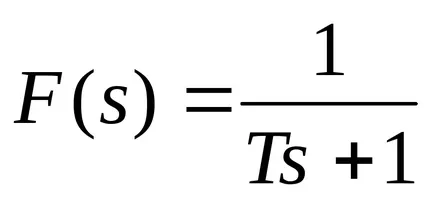
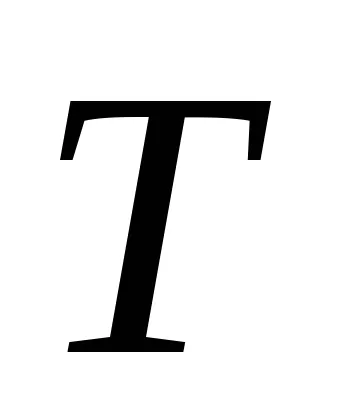
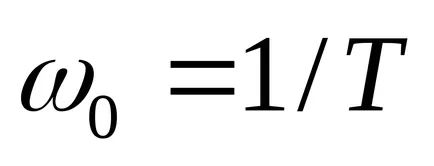
Unitatea oscilant are o funcție de transfer

, unde

- constanta de timp si

. frecvență

Frecventa nazyvaetsyasobstvennoy (naturalfrequency), un parametru

Parametrii de amortizare amortizare ilikoeffitsientom (dampingfactor). Cu o scădere

impuls și caracteristici tranzitorii devin caracter oscilatorie pronunțat, și apare pe „bizon“ AFC în zona de frecvență

. În cazul limită,

oscilații sunt neamortizate, și link-ul nazyvaetsyakonservativnym. Pe de altă parte, atunci când

sunt rădăcinile reale ale numitorul, iar unitatea devine elementul aperiodice în al doilea ordin.

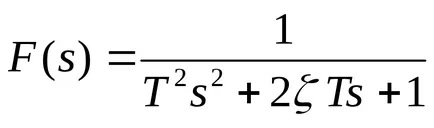
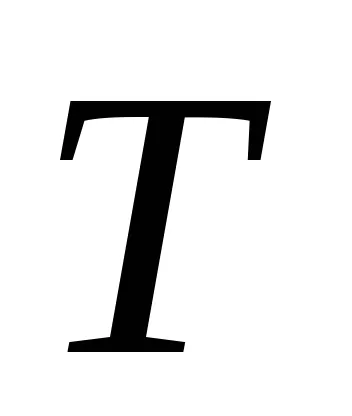
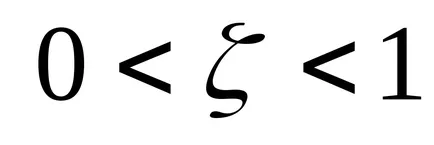
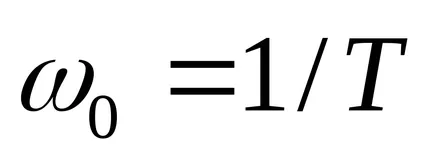
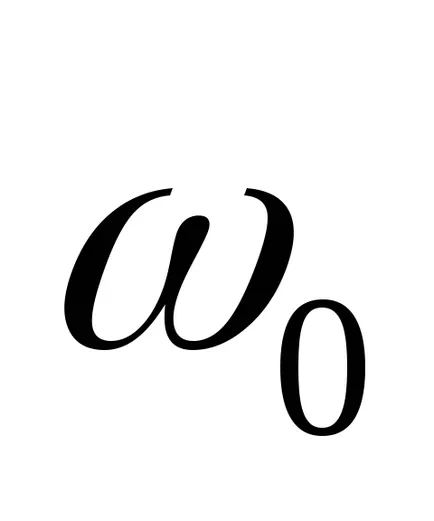
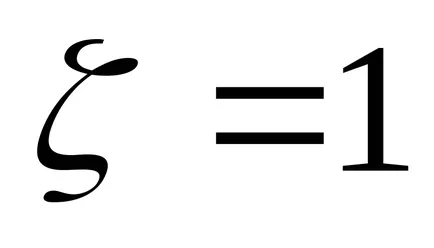
Pentru a găsi polii funcției de transfer f posibilitatea să utilizați

>> [w0, zeta, p] = umed (f)

Acesta vă permite să găsiți nu numai p pol. dar, de asemenea, chastotyw0 și factorii dempfirovaniyazeta ca matrice proprii corespunzătoare.

Zerourile funcției de transfer f se calculează ca

stabilitatea sistemului nu depinde de locația de zero-uri, dar ele influențează în mod semnificativ procesul de tranziție. echipă

construirea unei locații de pe hartă de zero-uri (care sunt indicate prin cercuri) și stâlpi (cruci), sisteme în planul complex.

Culoarea 1Chernym indicată de datele introduse de utilizator, un albastru - răspuns sredyMatlab.

2B literatura străină pentru sistemele unidimensionale utilizate sokraschenieSISO = SingleInputSingleOutput.

Funcția de transfer 3Polyusa sunt valori proprii ale matricei

. Astfel, în cazul în care funcția de transfer are un pol la punctul

, matrice

Acesta va degenera.

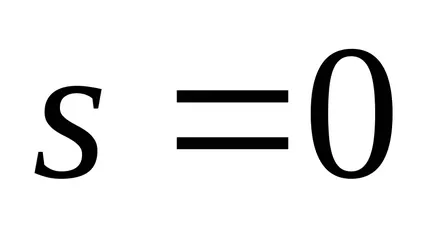
4Pentru sistemelor neliniare nu este adevărat.

5Znachenie

funktsieydamp se întoarce ca frecvența naturală pentru polul reală.