piramidă patrulateră în c2 problema

Rezolvarea problemei C2 de coordonate, mulți studenți se confruntă cu aceeași problemă. Ele nu pot calcula coordonatele punctelor. în formula produsului scalar. Cea mai mare dificultate este piramida. Și dacă punctul de bază sunt considerate a fi mai mult sau mai puțin, în mod normal, atunci partea de sus - un adevărat iad.

Astăzi vom face o piramidă patrulateră regulată. Există piramidă triunghiulară (alias - tetraedru). Aceasta este o construcție mai complexă, astfel încât o lecție separată va fi dedicată acestuia.

Pentru a începe cu noi amintim definiția:

Piramida Regular - este o astfel de piramidă, în care:

  1. La baza este un poligon regulat. Triunghi, pătrat, etc;
  2. Înălțimea, a avut loc la sol, trece prin centrul său.

În particular, baza este pătrat patrulateră piramidă. La fel ca Keops, doar un pic mai mic.

O reconciliere a piramidei, în care toate marginile sunt egale cu 1. Dacă problema nu este cazul, calculele nu se schimba - doar numărul va fi diferit.

Partea superioară a unei piramide patrulater

Deci, să presupunem că ni se dă dreptul patrulateră SABCD piramida. unde S - sus, ABCD jos - pătrat. Toate muchiile sunt 1. Trebuie să introduceți un sistem de coordonate și de a găsi coordonatele tuturor punctelor. Avem:

piramidă patrulateră în c2 problema

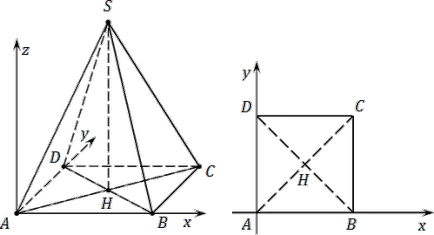
Introduceți sistem de coordonate cu originea sa, la punctul A.

  1. axa OX este paralelă cu muchia AB;
  2. OY axa - paralelă cu AD. Deoarece ABCD -, AB ⊥ AD pătrat;
  3. În cele din urmă, axa OZ este îndreptată în sus, perpendicular pe planul ABCD.

Acum avem în vedere coordonatele. Construcție: SH - înălțime, a avut loc la sol. Pentru comoditate, vom depune la baza piramidei la un desen separat. Deoarece punctul A. B. C și D minciună în OXY avionul. coordonarea lor z = 0. Avem:

  1. A = (0, 0, 0) - este originea;
  2. B = (1, 0, 0) - etapa 1 axa OX de origine;
  3. C = (1, 1, 0) - pasul 1 la OX axei și axa OY 1;
  4. D = (0, 1, 0) - Pas numai axa OY.
  5. H = (0,5; 0,5; 0) - Centrul de pătrat, segmentul de mijloc AC.

Rămâne să găsească coordonatele punctului S. De notat că coordonate x și y ale punctelor S și H sunt aceleași, deoarece acestea se află pe o linie paralelă cu axa OZ. Rămâne de a găsi z coordonate pentru punctul S.

Luați în considerare triunghiuri ASH si ABH.

  1. AS = AB = 1 condiție;
  2. Unghi AHS = AHB = 90 °, deoarece SH - înălțimea și AH ⊥ HB ca diagonala de pătrat;
  3. AH Side - totală.

Prin urmare, triunghiuri in unghi drept ABH și cenușă sunt pe un picior și un ipotenuză. Prin urmare, SH = BH = 0,5 · BD. Dar BD - diagonala unui pătrat cu latura 1. De aceea, avem:

Coordonatele totale ale punctului S.

În concluzie, vom scrie coordonatele tuturor nodurilor de piramida dreptunghiulare regulate:

Ce să faci când diferite fin

Ce se întâmplă dacă marginile laterale ale piramidei nu sunt egale cu marginile bazei? În acest caz, ia în considerare triunghiul AHS.

piramidă patrulateră în c2 problema

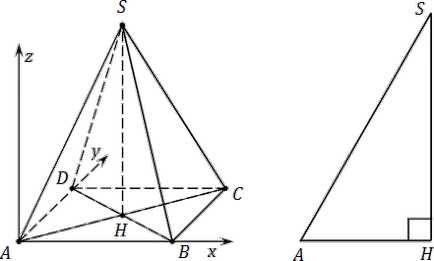
Triunghiul AHS - dreptunghiular. iar ipotenuza AS - este atât de margine laterală SABCD piramida originală. AH picior ușor considerat: AH = 0,5 · AC. SH picior Restul găsi teorema lui Pitagora. Acest lucru va coordona z pentru punctul S.

Sarcină. Dana regulat patrulateră piramida SABCD. la baza căruia este un pătrat cu latura 1. BS margine laterală = 3. Localizați coordonatele punctului S.

Coordonatele x și y ale punctelor pe care le cunoaștem deja: x = y = 0,5. Acest lucru rezultă din două fapte:

  1. Proiecția punctului S în planul OXY - punctul este H;
  2. În același punct de timp H - centrul ABCD de pătrat. toate acestea sunt părți 1.

Rămâne de a găsi punctul de coordonate S. Luați în considerare AHS triunghi. Este dreptunghiular, ipotenuza AS = BS = 3 catete AH - jumătate în diagonală. Pentru calcule, avem nevoie de o lungime:

Teorema lui Pitagora pentru triunghi AHS. AH 2 + SH 2 = AS 2. Avem:

Astfel, coordonatele punctului S.

  • Pregătirea gratuită pentru examenul de 7 lecții simple, dar foarte util + teme pentru acasă
  • piramidă patrulateră în c2 problema