Parametrii de bază cinematice

Concepte de bază ale rudelor ?? ematiki. Punct Keane ematika ??

Au o înțelegere de spațiu, timp, cale, cale, viteza și accelerația.

Cunoaște mișcarea punctului (natural și coordona) metode de referință.

Cunoaște decscrierea, relația parametrilor de mișcare Kin ?? EMA-matic, formulele de determinare ?? Eniya în curând-stey și accelerații (fără).

Kin ?? ematika consideră mișcarea ca circulând în pro-spațiu. Cauzele mișcării nu vor fi luate în considerare. Kin ?? ematika stabilește modalități de a specifica mișcarea și definește metodele determinate Eniya Kin ?? ?? ematicheskih parametrii de mișcare.

Traiectoria. Linia care delimitează un punct de material atunci când se deplasează în spațiu, numit traiectoria.

Calea trebuie să fie drepte și linia de plată și spațiu-stvennoj curba.

traiectoria Ecuația de mișcare plan: y = f (x).

Distanța parcursă. Calea măsurată de-a lungul traseului în direcția de mișcare. Denumire - S, - unități de metri.

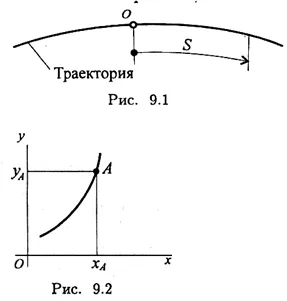
Ecuația de mișcare a unui punct. Ecuația care determină poziția punctului în mișcare în dependența de timpul, numită ecuația de mișcare.

Poziția punct la fiecare dată poate fi determinată, de distanța parcursă de turnare de-a lungul traseului de la un anumit punct fix, considerând-emoy ca referință (fig. 9.1). Această metodă de definire a mișcării se numește naturală.

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, ecuația de mișcare poate fi scrisă ca S = f (t). Poziția punctului poate fi determinată, de asemenea, dacă coordonatele sunt cunoscute bazate pe timpul (fig. 9.2). Apoi, în cazul deplasării în cele două ecuații trebuie să fie plan dat:

În cazul mișcării spațiale-TION se adaugă și a treia coordonate

Un astfel de proces se numește coordonate de referință de mișcare.

viteză. Vector cantitate ce caracterizează în prezent Snack-companie și direcția de mișcare de-a lungul traseului se numește viteză.

Viteza - vector în orice moment în timp este direcționat de-a lungul tangentei traiectoria-TION în direcția de mișcare (Figura 9.3.).

Dacă punctul de promo timp înfiorător egal trece distanță egală, mișcarea se numește uniformă.

Viteza medie pe calea AS este definită ca

unde # 916; S - distanța parcursă în timpul # 916; t; # 916; t - intervalul de timp.

În caz de egalitate la punctul intervale de timp trece mod inegal, mișcarea numită inegală.

În acest caz, viteza - este variabilă și depinde de timpul de v = f (t).

Atunci când se analizează intervalele de timp mici (# 916; t → 0) Viteza media-NJ devine egal cu adevărat momentul dat vitezei-ny. Din acest motiv, în momentul în care viteza este definită ca

derivat al modului în timp:

Unitatea de viteză ia 1 m / s. Uneori Viteza este măsurată, dizolvată în km / h, la 1 km / h = 0,278m / s.

Punct de accelerare. Cantitatea de stoc caracterizează viteza ratei de schimbare ??-lea și direcția cantități, numit punct de accelerație.

Punct de viteză în timp ce se deplasează de la punctul de M1, M2 până la un punct de pe UI-lea nyaetsya valoare ?? și direcția. Valoarea medie a accelerației într-un interval de timp dat

Atunci când se analizează o perioadă de timp infinitezimal accelerația medie în accelerare rândul său, la mo-ment:

De obicei, pentru comoditatea considerării două reciproc perpen-dikulyarnye componentele accelerației: (. Figura 9.5) normală și tangențială.

accelerație normală în sus caracterizează viteza de schimbare a direcției și este definită ca

unde r - raza de curbură a traiectoriei la un moment dat.

accelerație normală când tu ?? îndreptat în întregime perpendicular SKO-creștere într-un centru al arcului.

tangențiale de accelerare la viteză caracterizează schimbarea valorilor ?? e ?? atunci când tu și toate îndreptate la o tangentă la calea; când accelerarea direcția coincide cu direcția vitezei, iar în timpul decelerării este îndreptată opusă direcției de torusului Century viteză.

Formula de determinare ?? Eniya accelerare tangențială este:

Valoarea este definită ca accelerația completă AT = dV / dt = v 1 = S '' (fig. 9.6).