oscilație liberă

pendul matematic numit dimensiuni mici, suspendat pe un fir inextensibil subțire, masa care este neglijabilă în comparație cu corpul de masă. În poziția de echilibru, atunci când pendulul atârnă plumb, forța de gravitație echilibrat de tensiunea firului Când devierea pendulului din poziția de echilibru la un φ unghi apare componenta tangențială a forței de gravitație Fτ = -Mg păcat φ (Fig. 2.3.1). „Minus“ semn în această formulă înseamnă că componenta tangențială îndreptată în direcția opusă devierea pendulului.

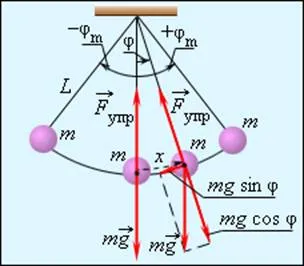
Pendulum. φ - deviația unghiulară a pendulului din poziția de echilibru, x = l φ - deplasare de-a lungul arcului pendulului

Dacă x reprezintă deplasarea liniară a pendulului din poziția de echilibru a lungul arcului de cerc de rază l. deplasarea unghiulară este egală cu φ = x / l. A doua lege a lui Newton, înregistrată pentru proiecțiile de accelerare și forță în direcția tangentei, dă:

Acest raport arată că pendulul matematic este un sistem neliniar complex, deoarece forța tinde să revină pendulului la poziția sa de echilibru, este proporțională nu la deplasarea x. și

Numai sluchaemalyh vibrații când priblizhennomozhno înlocui namatematichesky pendul este un oscilator armonic. t. e. un sistem capabil să execute vibrații armonice. În practică, această apropiere este valabilă pentru unghiurile de ordinul a 15-20 °; atunci când această valoare este diferită de cel mult 2%. Pendulul cu amplitudini mari nu sunt armonice.

Pentru mici oscilații balansoare matematice a doua lege a lui Newton poate fi scrisă ca

Astfel, accelerația tangențială aτ pendulului este proporțională cu deplasarea x. luate cu semnul opus. Aceasta este exact starea în care sistemul este un oscilator armonic. Ca regulă generală pentru toate sistemele care pot face coeficient liber armonic de proporționalitate între modulul de oscilație a accelerației și deplasarea din poziția de echilibru este egală cu pătratul frecvenței unghiulare:

Această formulă exprimă frecvența naturală a oscilații mici ale unui pendul matematic.

Orice organism înfipt o axă de rotație orizontală, se poate realiza într-un gravitaționale oscilații libere de câmp și, prin urmare, de asemenea, pendulul. Un astfel de pendul se numește fizic (Fig. 2.3.2). Acesta diferă de numai distribuția masei matematice. Poziția stabilă centrul masei de echilibru C este mai mic decât fizic rotație pendul axa O pentru linia verticală care trece prin axa. În cazul unui unghi al pendulului φ are loc în momentul gravitației, pendulul tinde să revină la poziția sa de echilibru:

„Minus“ semn în această formulă, ca de obicei, aceasta înseamnă că cuplul tinde să se transforme pendulului în direcția opusă a abaterii de la poziția sa de echilibru. Ca și în cazul unui pendul simplu care returnează momentul M este proporțională. Acest lucru înseamnă că numai la unghiuri mici, atunci când pendul fizic capabil să execute oscilații libere de armonice. În cazul fluctuațiilor mici

și a doua lege a lui Newton pentru un pendul fizic ia forma

unde ε - accelerația unghiulară a pendulului, I - momentul de inerție al pendulului în raport cu axa de rotație O. Coeficientul modulului de proporționalitate între deplasare și accelerația este egală cu pătratul frecvenței unghiulare:

Aici ω0 - frecvența naturală a oscilații mici ale unui pendul fizic.

O derivație mai riguroasă a formulelor pentru ω0 și T se poate face, dacă luăm în considerare relația matematică dintre accelerația unghiulară și dezaxarea unghiulară: unghiulară ε accelerația este derivata a doua a cp unghiulare la timp:

Prin urmare, ecuația care exprimă a doua lege a lui Newton pentru un pendul fizic, poate fi scris ca

Această ecuație este liber de oscilații armonice.

în această ecuație are semnificația unui coeficient pătrat frecvențe circulare de oscilații armonice ale unui pendul fizic.

Conform teoremei de deplasare paralelă cu axa de rotație (teorema lui Steiner) moment de inerție I poate fi exprimată prin momentul de inerție IC în jurul unei axe care trece prin centrul C al maselor pendulului și paralelă cu axa de rotație:

În cele din urmă, pentru ω0 pulsația oscilațiilor libere ale unui pendul fizic următoarea expresie: