O cutie - imaginea 186405-13

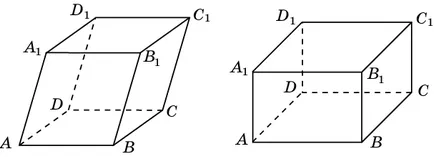
Paralelipiped. Paralelipiped este numit un poliedru, a cărei suprafață este format din șase paralelograme. Se numește paralelipiped cuboid ale căror fețe - dreptunghiuri. De obicei, o cutie este afișată după cum se arată în figură. Și anume, trase paralelogram ABB1A1, ilustrând una dintre fețele cutiei, și este egală cu paralelogram DCC1D1, laturile care sunt paralele cu laturile ABB1A1 paralelogramului. vârfuri ale acestor Respectivii paralelogram sunt conectate prin segmente. Segmentele care descriu marginile invizibile ale cubului, a avut loc o linie punctată. În cazul unui paralelipiped, în loc de paralelograme, care prezintă două fețe sunt desenate în dreptunghiuri egale.

Poza 13 de prezentare „poliedre“

Dimensiuni: 607 x 219 pixeli, formatul: png. Pentru a descărca imaginea pentru lecția de geometrie, faceți clic pe butonul mouse-ului dreapta imagine și faceți clic pe „Save Image As. “. Pentru a afișa imagini în clasă, puteți descărca, de asemenea, prezentarea „Mnogogranniki.ppt“, în întregime, cu toate imaginile din zip-arhivă. Mărime fișier - 602 KB.

prezentarea Related

„Proprietățile unui paralelipiped“ - directă. 1. Toate fețele - paralelogram. Formulați proprietăți paralllelepipeda. Dovedește: Definiți caseta. Nu este dreptunghiular. Scrierea definiție prismă. Subiect nou. Nu cuburi. Dreptunghiular. Înclinat. Rezumând rezultatele. Cuboid cu margini egale se numește un cub. Rezolvarea problemelor.

„Secțiunile transversale a cutiei» - PSKR - secțiune a casetei. Rulați construi secțiuni ale casetei în următoarele cazuri: Setare. construi o secțiune care trece prin punctele M, N, K. Dreptunghi CKK'C '- secțiunea ABCDA'B'C'D'. MNPKL - box-secțiunea ABCDA'B'C'D“. Dreptunghi ADKN - secțiunea ABCDA'B'C'D“. Sarcină. construi o secțiune care trece prin punctele M, N, K. M. (ABB'A ') N. (ABCD) K. CC'.

„Tetrahedron și o cutie“ - Elemente ale tetraedru. Efectuat Kotlovskaya I.Yu.g.N.Novgorod. Diagonalele se intersectează și se împărtășesc punctul de intersecție a două. caseta Proprietăți. Secțiunea. Tetraedru. Secțiunea. cutie tetraedru. 1.Protivopolozhnye fețele sunt paralele și egale. construcția secțiunii.

„Volumul cutiei“ - În volum vechi unitate de Babilon au fost cuburi. Sarcini pentru materialul de fixare. Sarcina №1. Chiar și în cele mai vechi timpuri, oamenii au nevoie pentru a măsura cantitatea de orice substanță. Ia volumul cubului, al cărei margine este de 3 cm. Unitate de volum egal cu 1 dm3 numit litru. Lecția Subiect: Volumul cutiei.

„Caseta 5 clasă“ - Construcția cutiei. Să vedem dacă te-ai uitat cu atenție. Cuboid. La cuboid 12 margini și 8 vârfuri. Cutie de chibrituri, o bucată de lemn, caramida da o idee a unui paralelipiped dreptunghic. Dreptunghiular. fețele de mână sunt numite marginile paralelipipedul, și se confruntă cu partea de sus - partea de sus a casetei.

„Lectia paralelipiped dreptunghiular“ - Construirea unui dreptunghi de lungime predeterminată (a) și înălțimea (h). Paralelipiped. Calculul Mental. Cuboid. Înălțime. Scanare. Conectați capetele segmentelor, linia invizibilă - linia punctată. Sarcina № 2. Înălțimea paralelipiped dreptunghic este de 2,4 dm. Măsurarea. Scop: Un algoritm pentru construirea unui cuboid.

poliedru

29 prezentări ale poliedrului