Numerele raționale și iraționale

Am arătat anterior că $ 1 \ frac25 $ - aproape de $ \ sqrt2 $. În cazul în care este exact egală cu $ \ sqrt2 $, problema va fi rezolvată. Apoi relația - $ \ $ Frac, care poate fi transformată într-un raport de numere întregi $ \ frac75 $, multiplicând părțile superioare și inferioare ale fracțiunii 5, și ar fi cantitatea necunoscută.

Din păcate, $ 1 \ frac25 $ nu este o valoare exactă a $ \ sqrt2 $. Un răspuns $ 1 \ $ Frac mai precis, ne dă raportul $ \ frac $. Chiar și mai multă acuratețe vom realiza atunci când acesta este egal cu $ \ sqrt2 $ 1 la $ \ frac $. În acest caz, raportul în numere întregi este egal cu $ \ frac $. Dar $ 1 \ frac $ nu este o valoare exactă a rădăcinii pătrate a 2. matematicieni greci au petrecut o mulțime de timp și efort pentru a calcula valoarea exactă a $ \ $ sqrt2, dar că acestea nu au reușit. Ei au fost în măsură să furnizeze raportul $ \ frac $ ca un raport de numere întregi.

În cele din urmă, marele matematician grec Euclid a demonstrat că, indiferent de modul în care precizia sporită a calculelor, pentru a obține valoarea exactă a $ \ $ sqrt2 imposibil. Nu există nici o astfel de fracțiuni, care atunci când este ridicat în piață, va avea ca rezultat 2. Se spune că mai întâi a ajuns la această concluzie prin Pitagora, dar acest fapt inexplicabil atât om de știință impresionat, el a promis să se și au depus jurământul cu ucenicii săi să păstreze descoperirea unui secret . Cu toate acestea, este posibil, această informație nu corespunde realității.

Dar, în cazul în care numărul de $ \ frac $ nu poate fi reprezentat ca un raport de numere întregi, atunci orice fracție. conținând $ \ $ sqrt2, de exemplu, $ \ frac $ sau $ \ frac $, de asemenea, nu poate fi reprezentat ca un raport de întregi, deoarece toate aceste fracții pot fi convertite în $ \ frac $, înmulțit cu un număr de zile. Deoarece $ \ frac = \ frac \ ori \ frac12 $. Sau $ \ frac \ ori 2 = 2 \ Frac $, care poate fi transformată prin înmulțirea părțile superioare și inferioare pe $ \ $ sqrt2, și a obține $ \ frac $. (Nu trebuie să uităm că, indiferent de ceea ce este numărul $ \ $ sqrt2, dacă vom multiplica de $ \ sqrt2 $, obținem 2)

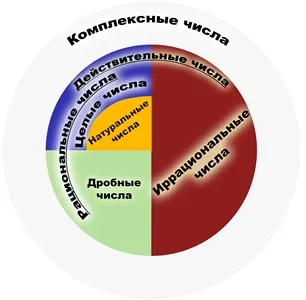
Pe măsură ce numărul de $ \ $ sqrt2 nu poate fi reprezentat ca un raport de numere întregi, se numește un număr irațional. Pe de altă parte, toate numerele care pot fi reprezentate ca un raport de numere întregi sunt numite raționale.

Rational sunt toate numere întregi și fracții, atât pozitive, cât și negative.

După cum sa dovedit, de cele mai multe rădăcini pătrate sunt numere iraționale. Raționale rădăcini pătrate au doar numere incluse în numărul de numere pătrate. Aceste numere sunt numite și pătrate perfecte. Numerele raționale sunt, de asemenea, o fracțiune formată din aceste pătrate perfecte. De exemplu, $ \ sqrt $ este un număr rațional, ca $ \ sqrt = \ = frac \ frac43 $ 1 sau $ \ frac13 $ (4 - este rădăcina pătrată a 16, și 3 - rădăcina pătrată din 9).

Conținut legat de:

Împărtășește cu prietenii: