număr complex

Numere complexe [1] - extinderea setului de numere reale. de obicei, notată \ (\ mathbb \). Orice număr complex poate fi reprezentat ca o sumă formală \ (x + iy \), în cazul în care \ (x \) și \ (y \) - numere reale, \ (i \) - unitatea imaginară. care este unul dintre numerele care satisfac ecuația \ (i ^ 2 = -1 \). În general pronunția acceptată este un număr complex. deși număr complex este pronunțat, de asemenea, găsit.

Numerele formă complexă câmp algebric închis - ceea ce înseamnă că gradul de polinomului \ (n \) cu coeficienți complecși are exact \ (n \) rădăcini complexe, adică corect teorema algebra de bază.

Definiții [citare]

Standard [citare]

Formal, numărul de complex \ (z \) - este o pereche ordonată de numere reale \ ((x, y) \), cu le introduse după cum urmează operațiile de adunare și înmulțire:

Imaginar unitate într-un astfel de sistem reprezentat de o pereche \ (i = (0,1) \, \). Prin urmare, determinarea eronată a numărului \ (i \), ca singurele numere care satisfac ecuația \ (i ^ 2 = -1 \), deoarece numărul \ ((-i) \) satisface, de asemenea, această ecuație. De asemenea, trebuie remarcat faptul că exprimarea formei \ (i = \ sqrt \) incorect. ca rădăcină algebrică este definit într-un set de numere întregi non-negative.

Matricea [citare]

Numerele complexe pot fi, de asemenea, definit ca o familie de matrici reale de forma $$ \ începe x y \\ -y \; \; x \ end $$ cu adăugarea matricei obișnuită și multiplicarea. Unitatea actuală se va potrivi $$ \ începe 1 0 \\ 0 \; \; 1 \ end $$. imaginar unitate - $$ \ începe 0 1 \\ -1 \; \; 0 \ end $$

Toate aceste definiții conduc la extensii izomorfe ale numerelor reale \ (\ mathbb \), la fel ca orice alte extinderi ale polinoame structura câmpului x² 1

Acțiunea privind numerele complexe [necesită citare]

Determinarea Related [citare]

variabilă complexă este de obicei notată \ (z \). Să \ (x \) și \ (y \) sunt numere reale, astfel încât \ (z = x + iy \). atunci

Reprezentarea numerelor complexe [necesită citare]

Formularul algebric [citare]

Înregistrarea complex număr \ (z \) a \ (x + iy \) \ (x, y \ in \ mathbb \), numita formă algebrică a numărului complex.

Suma și produsul numerelor complexe pot fi calculate direct prin multiplicarea și însumarea acestor termeni, ținând cont de identitatea \ (i ^ 2 = -1 \).

Trigonometrică și exponențială forma [citare]

Dacă reale \ (x \) și imaginar \ (y \) a unui număr complex exprimat în termeni de unitate \ (r = | z | \), și argumentul \ (\ varphi \) (\ (x = r \ cos \ varphi \), \ (y = r \ păcat \ varphi \)), numărul complex \ (z \) pot fi scrise sub forma trigonometric $$ z = r (\ cos \ varphi + i \ păcatul \ varphi). $$ poate fi util următoarea notației numere complexe, este strâns legată de termenii trigonometrice cu formula $$ z = re Euler ^, unde $$ \ (e ^ \) - expansiunea exponențială pentru cazul exponent complex.

Reprezentarea geometrică [necesită citare]

Dacă pe planul axa X este partea reală, iar axa verticală - imaginar, numărul complex va corespunde unui punct cu coordonate carteziene \ (x \) și \ (y \) (sau de raza, care este același) și modul și argumentul va fi coordonatele polare ale punctului.

Reprezentarea geometrică a numerelor complexe corespunde sumei sumei vectorului a vectorilor corespunzători. Când inmultirea numerelor complexe multiplicate sunt adăugate module și argumentele lor. Prin urmare, în special, obținem formula Moivre.

Formula permite construirea puterea unui număr complex reprezentat în formă trigonometric. DeMoivre formula are forma: $$ z ^ n = [r (<\href<\texttip <Косинус>>> \ varphi + i \ păcatul \ varphi)] ^ n = r ^ n (\ cos n \ varphi + i \ păcatul n \ varphi), $$

George Alexandrov a găsit forma cea mai generală a formulei DeMoivre: $$ (x + y \, i) ^ n = \ sqrt \ bigg [\ cos \ bigg (\ fracturate frac \ frac \ + n \ operatorname> \ bigg) + i \ , \ frac \ păcat \ bigg (\ fracturate frac \ frac \ + n \ operatorname> \ bigg) \ bigg] $$

unde x, y, n - orice număr real.

Conjugatul [regula]

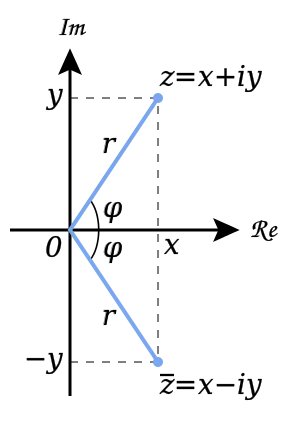
Reprezentarea geometrică a numerelor de conjugat

Istoricul [modifică]

Pentru prima dată, se pare că, cantitățile imaginare a apărut în celebra lucrare „Marea artă, sau un“ reguli algebrice Cardano (1545), care au găsit-l improprii pentru consum.

Favoarea cantități imaginare, în special, la decizia ecuației cubice, cazul ireductibilă așa-numitul (exprimate în termeni de rădăcini reale de rădăcini cubice de valori imaginare), mai întâi estimat Bombelli (1572). El a dat, de asemenea, câteva reguli simple pentru operații cu numere complexe.

Expresiile de forma \ (a + b \ sqrt \), care apar în soluția de ecuații pătratice și cubice, a devenit cunoscut sub numele de „imaginar“, în secolele XVI -XVII secole, dar chiar și pentru mulți dintre marii savanți ai algebric secolul XVII și natura geometrică a cantităților imaginare este neclară. Este cunoscut, de exemplu, că Newton nu a inclus valoarea conceptului de numere imaginare, și Leibniz face parte din fraza: „Numerele imaginari - acesta este un refugiu mare și minunată a spiritului divin, aproape existență amfibie din neant“ [Sursa? ].

Problema expresiei rădăcinilor grad \ (n \) din numărul dat a fost practic rezolvată în DeMoivre (1707) și Coats (1722).

Simbol \ (i = \ sqrt \) oferit de Euler (1777 publ. 1794), care a dus la prima literă a cuvântului imaginarius. El a declarat în 1751 ideea închiderii algebrică a câmpului numerelor complexe. Aceeași concluzie a fost atins de către D'Alembert (1747), dar prima dovadă riguroasă a acestui fapt aparține Gauss (1799). Gauss și puse în utilizarea pe scară largă, termenul „număr complex“ în 1831, deși termenul a fost folosit în același sens ca și matematicianul francez Lazare Carnot în 1803.

Interpretarea geometrică a numerelor și a operațiunilor de pe ele complexe, a apărut pentru prima dată în lucrarea lui Wessel (ing.). (1799). Primii pași în această direcție au fost făcute Wallis (Anglia) în 1685.

Teoria aritmetică a Hamilton (1837) a fost construit numere complexe ca perechi de numere reale. De asemenea, el face parte o generalizare a numerelor complexe - cuaternionii. algebra comutativă asta.