Neomogene ecuații diferențiale liniare cu coeficienți aleatoare
Să considerăm ecuația formei
Cu notația putem scrie:
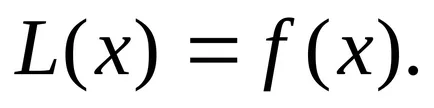
În acest caz, presupunem că coeficienții și partea dreaptă a acestei ecuații sunt continue într-un anumit interval (finit sau infinit).
Teorema.Obschee soluție a ecuației diferențiale liniare neomogene într-o regiune este suma tuturor deciziilor sale și soluția generală a ecuației diferențiale liniare omogene corespunzătoare.
Dovada. Fie Y - o soluție a ecuației neomogene.
Apoi, prin această soluție înlocuind în ecuația originală obținem identitatea:
lăsa
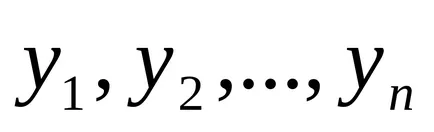
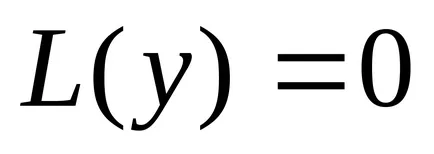
În continuare ne arată că suma soluției generale a ecuației neomogene.

În general, soluția Y poate fi obținută din soluția generală, deoarece Este o soluție particulară.
Astfel, în conformitate cu această teoremă pentru a rezolva o ecuație diferențială liniară neomogen trebuie să găsim o soluție generală a ecuațiilor omogene corespunzătoare și o modalitate de a găsi o soluție particulară a ecuației neomogene. De obicei, este de selecție.
Este convenabil să se utilizeze metoda variatiei constantelor arbitrare.
Pentru aceasta, mai întâi găsiți soluția generală a ecuației omogene corespunzătoare în forma:
Apoi, presupunând koeffitsientyCifunktsiyami marunti, căutăm o soluție a ecuației neomogene:
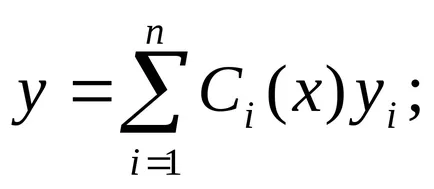
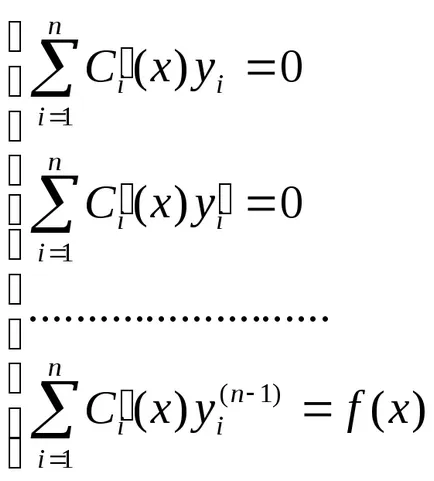
Exemplu. rezolva ecuația
Rezolvarea ecuație liniară omogenă
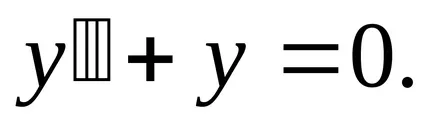
Soluția ecuației neomogene va arata:
Constitui un sistem de ecuații:
Noi rezolva acest sistem:
Din relația găsi funktsiyuA (x).
Acum vom găsi B (x).
Substitut valorile obținute în soluția generală a ecuației formula neomogene:
Astfel, a fost posibil să se evite găsirea unei soluții particulară a ecuației neomogene prin încercare și eroare.
In general, metoda variatiei constantelor arbitrare potrivite pentru găsirea de soluții pentru orice ecuație liniară neomogenă. dar, pentru că găsirea sistemul fundamental de soluții ale ecuației omogene corespunzătoare poate fi o provocare, această metodă se aplică în principal ecuații neomogene cu coeficienți constanți.
Neomogene ecuații diferențiale liniare cu constante
Ecuația cu partea dreaptă a unui tip special.
Este posibil să ne imaginăm forma unei anumite soluții în funcție de tipul de partea dreaptă a ecuației neomogene.
Există următoarele cazuri:
I. Partea dreaptă a ecuației diferențiale liniare neomogene are forma:
în cazul în care - stepenim polinom.
Apoi, o soluție specială este solicitată sub formă de:
Aici, Q (x) - un polinom de același grad ca și P (x). dar cu coeficienți nedeterminate și r - un număr care indică de câte ori numărul este rădăcina ecuației caracteristice ecuației diferențiale liniare omogene corespunzătoare.
Exemplu. rezolva ecuația
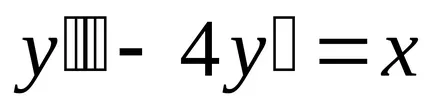
Noi rezolva ecuația omogenă corespunzătoare:
Acum vom găsi o soluție particulară a ecuației neomogena originală.
Să comparăm pe partea din dreapta-dreapta cu care se confruntă, discutat mai sus.
Soluția particulară este solicitată în forma în care
Acum definim coeficienții necunoscuți A și B.
Înlocuind o anumită soluție în formă generală în ecuația diferențială inițială neomogen.
Soluție totală parțială:
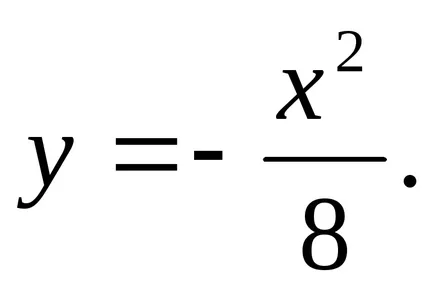
Apoi, soluția generală a ecuației diferențiale liniare neomogene:
II. Partea dreaptă a ecuației diferențiale liniare neomogene are forma:
Apoi, o soluție particulară a ecuației neomogene va arata:
în cazul în care numărul de r arată cât de multe ori numărul de
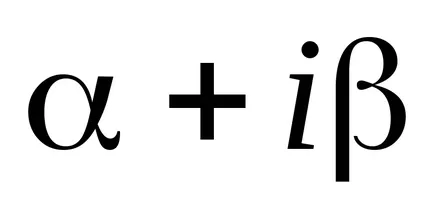
Rețineți că, în cazul în care partea dreaptă a ecuației este o combinație de expresii de tipul discutat mai sus, soluția este o combinație de soluții ale ecuațiilor auxiliare, fiecare dintre acestea fiind partea dreapta care corespunde expresiei combinației.
Ie dacă ecuația este de forma, apoi o soluție particulară a acestei ecuații este
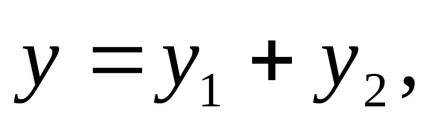
Pentru a ilustra un exemplu rezolva o altă metodă discutată mai sus.
Exemplu. rezolva ecuația
Compoziția și rezolva ecuația caracteristică: