minimul necesar
1.Dispersiya
Dispersia - caracteristici ale variabilelor aleatoare, definite ca așteptarea pătratul abaterii unei variabile aleatoare de la așteptările sale.
varianța teoretică este o măsură a răspândirii distribuției de probabilitate. Acesta este definit ca așteptarea a diferenței pătrat dintre valoarea


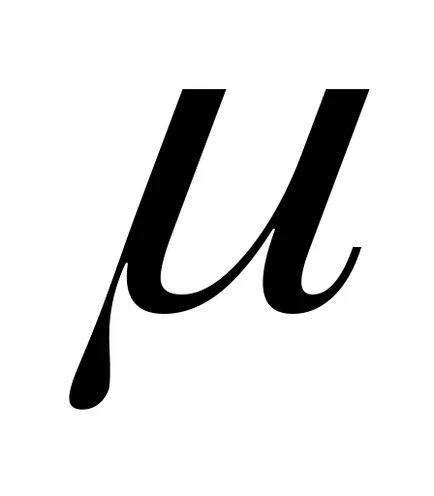


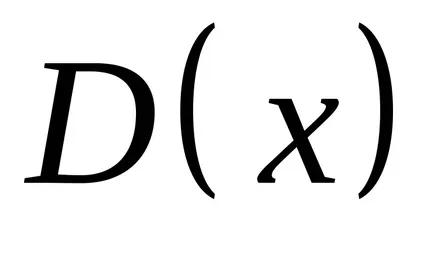
.
din
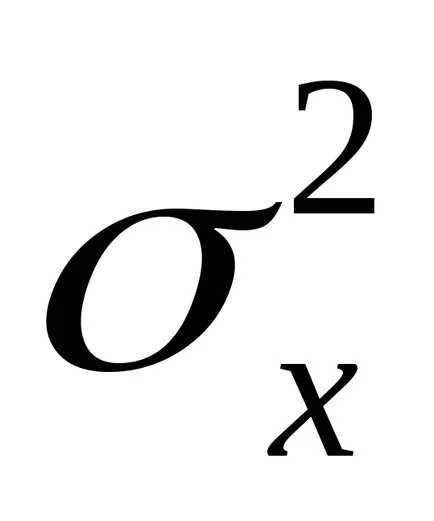

valoare



2.Mat. așteptare
Așteptarea - suma produselor de valori ale variabilei aleatoare la probabilitățile corespunzătoare.
Așteptarea unei variabile aleatoare discrete - este o medie ponderată a tuturor valorilor posibile ale acesteia, în care un factor de ponderare este luată ca probabilitatea rezultatului corespunzător. Puteți calcula prin înmulțirea toate valorile posibile ale unei variabile aleatoare pe probabilitatea lor și însumarea produsului rezultat. Matematic, în cazul în care variabila aleatoare este desemnat ca


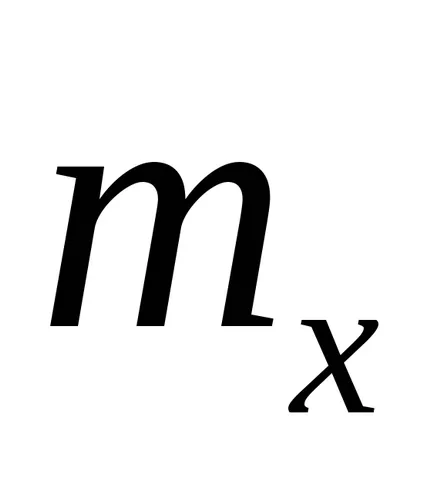
Să presupunem că
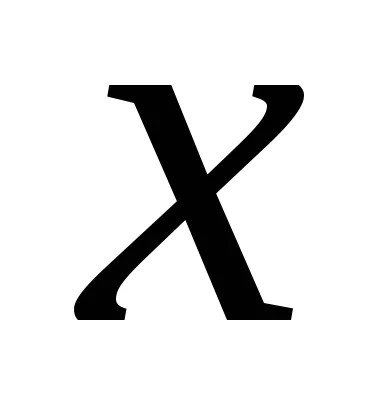


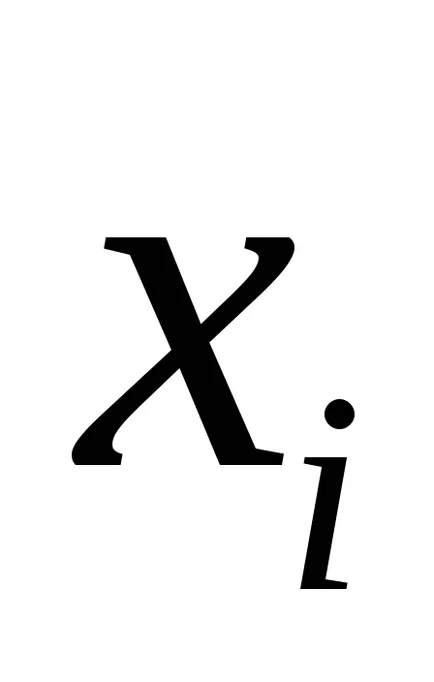

.
Așteptarea matematică a unei variabile aleatoare este adesea menționată ca media sa pe întreaga populație. Pentru o variabilă aleatoare
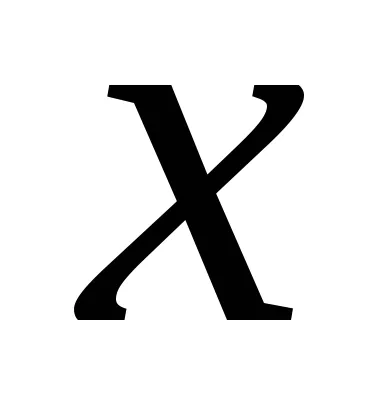

Așteptările funcții variabile aleatoare discrete
lăsa

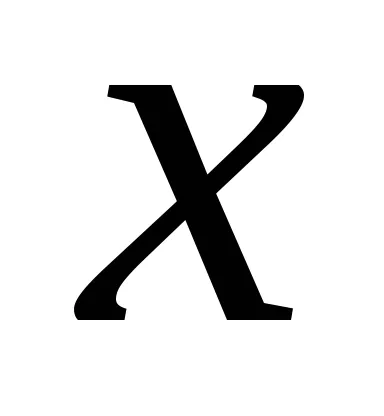


,
în cazul în care însumarea este peste toate valorile posibile

Reguli pentru calcularea speranța matematică
Există trei reguli care sunt adesea folosite. Aceste reguli sunt aproape de la sine înțeles, iar acestea sunt aplicabile în egală măsură variabile aleatoare discrete și continue.
Articolul 1. Așteptarea suma mai multor variabile este egală cu suma așteptărilor lor matematice. De exemplu, în cazul în care există trei variabile aleatoare



.
Regula 2. Dacă variabila aleatoare este înmulțită cu o constantă, atunci așteptarea sa este înmulțită cu aceeași constantă. dacă
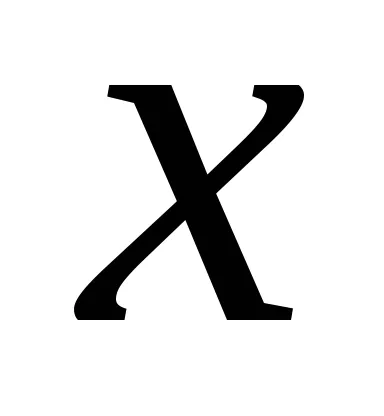

.
Regula 3. Așteptarea constantă acolo ea. De exemplu, dacă

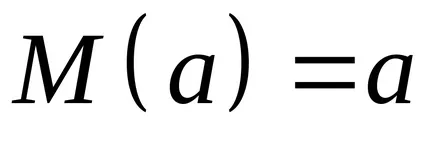
Ancheta a celor trei reguli:
.
Covarianță - caracteristica numerică a distribuției în comun a două variabile aleatoare, egală cu așteptarea produsului abaterilor de variabile aleatoare de la așteptările lor matematice.
Puteți utiliza următoarele formule gata făcute, care urmează direct din soluția sistemului (1.4):
în cazul în care - semne de covarianță





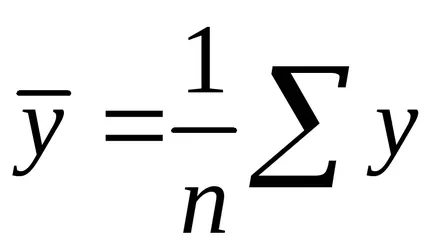


4.Korrelyatsiya
Coeficientul de corelație sau un coeficient de corelație pereche - o măsură de modificări în natura a două variabile aleatoare. Coeficientul de corelație este notat cu litere latine
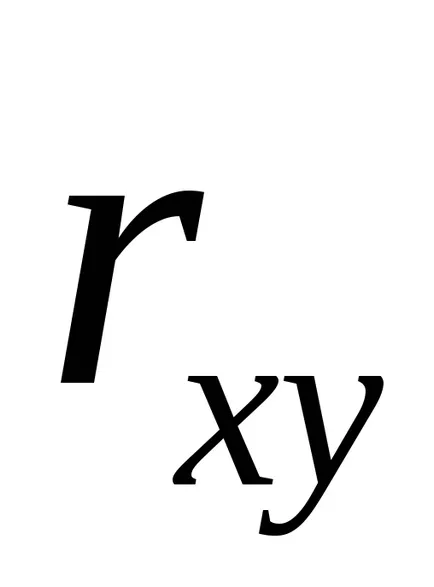
Ecuația de regresie este întotdeauna completată de o apropiere indicator al conexiunii. Atunci când se utilizează regresie liniară ca un indicator al unor astfel de acte de coeficienți de corelație liniară
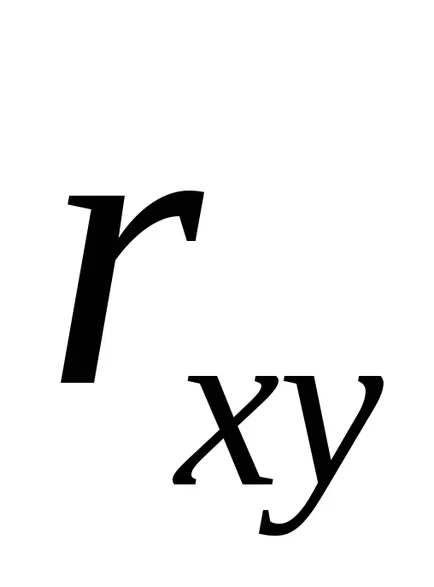
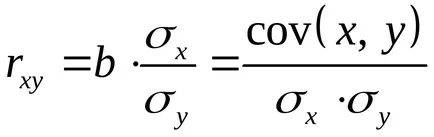
Coeficientul de corelație liniară este în intervalul:
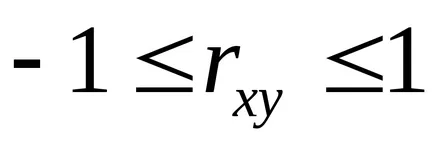

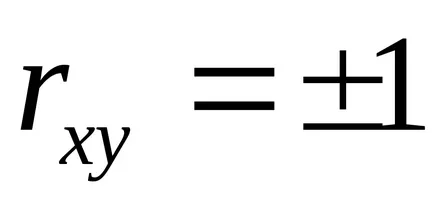
Pentru a evalua calitatea selectarea unei funcții liniare se calculează pătrat coeficientului de corelație liniară
