Mikel Alberta - lumea matematicii

Maestrul indică efectuat inexact în construcția tangenta pentagrama.

Acesta este într-adevăr cazul. Stapanii au intrat steaua cu cinci colțuri într-un inel a cărui rază este determinată vizual. În cazul în care rezultatul de construcție diferită de așteptat, comandantul corectat eroarea, dar nu prin metoda „Kira-Kira“, iar în ochi, nu în urma unor metode bine definite, care în mod necesar ar conduce la soluția dorită.

M-am gândit cum să ajute stăpânii în această sarcină. Era evident că acesta a fost construirea de cinci puncte echidistante pe circumferință, care sunt apoi îmbinate în perechi, pentru a forma o pentagramă. În consecință, problema se reduce la construirea unui pentagon regulat. Soluția propusă de Euclid, nu este potrivit pentru două motive. În primul rând, se părea inutil să atragă un pentagon pe perete Toraja folosind metoda greoaie de Euclid, pe care nu-mi amintesc toate detaliile. În al doilea rând, nu este etic să aducă această metodă într-o altă cultură. Și apoi ... Eureka! De ce să nu încercați să rezolve problema într-o manieră caracteristică a unei culturi în care nu a existat această sarcină? Cu alte cuvinte, este posibil să se aplice „Kira-Kira“ metoda de a construi poligoane regulate? Răspunsul la această întrebare este da, dar nu chiar la fel ca s-ar fi sugerat un matematician european.

Ni se dă un cerc, în care dorim să scrie un pentagon regulat.

Vom aplica metoda „Kira-Kira“, pune pe un raft de bambus cincime din circumferința. Apoi, pe circumferință amâna cinci segmente etalon obținute: P 0 P 1 P 1. P 2 .... P 4 P 5. În cazul în care sfârșitul ultimului segment coincide cu punctul P 0. respectiv primul și ultimul punct sunt aceleași, de închidere a ciclului, marcat de cinci puncte de contact sunt nodurile unui pentagon regulat. Coarda strângere cinci arce circulare corespunzătoare acestor cinci puncte care sunt părți la pentagonul dorită. Pentru a construi o pentagramă, suficient pentru a conecta puncte după cum este necesar.

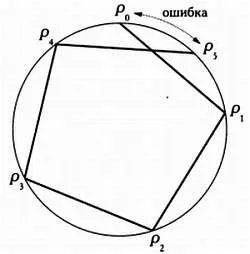
În cazul în care bucla nu este închisă, adică, în cazul în care R5 nu este același lucru ca și P 0. Aceasta înseamnă că am făcut o greșeală. La început am crezut că această eroare ar trebui să fie corectate, găsind-o un al treilea, cu ajutorul unei șipci de bambus, și apoi adăugați-l la lungimea inițială a segmentului (sau scade din). Dar nu a ajutat la îmbunătățirea rezultatului. Cum de a rezolva problema? Eureka! Am lucrat cu puncte de pe cerc, dar încă utilizate segmentele, în timp ce am avut de a corecta o greșeală făcută atunci când rafturi arc. A trebuit să acorde o atenție să nu personalului, pe care am pus deoparte coarda și a arcului de cerc care corespunde valorii erorii.

Totul este clar: este necesar să ia în considerare cercul ca un segment. Securizarea un capăt al raftului, la un al doilea punct, marcat pe cerc, m-am mutat la celălalt capăt al cremalierei, care, în opinia mea, ar fi fost la sfârșitul celei de a treia parte a arcului corespunzător greșeala lui. Ca rezultat, am primit o nouă lungime coardă.

pentru a aborda laicilor-cheie în faptul că toate semnele de pe raftul de bambus corespund acorduri și arce ... Evrika! Arcul electric rezultat trebuie să fie suma arcurilor. Dacă adăugați o coardă ca segmentele, acesta nu este cazul - arcul rezultată nu va fi egală cu suma celorlalte două. Cu alte cuvinte, suma va fi egală cu coarda coardă rezultată, numai dacă definim ca suma a corzilor coardă egală cu latura triunghiului, care a fost construit pe cele două acordurile inițiale:

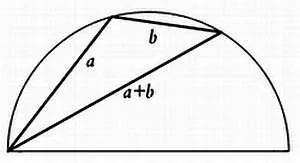
Am identificat un algoritm non-euclidiene recursiv pentru construirea poligoane regulate, așa cum am descris-o metodă aplicabilă atunci când împărțirea cercului în n părți. În plus, am identificat un grup nou aditiv, pe care o numim „acorduri de grup ale cercului.“ Suma celor două coarde are sens, dacă vom defini ca o latură a triunghiului, care a fost construit pe coardă originală - în acest caz, arcul rezultat este egal cu suma celor două arce inițiale. Metoda „Kira-Kira“ a fost suficient de flexibil, care poate fi utilizat în rezolvarea sarcinilor pentru care nu a fost destinat.

Construirea enneagon dreapta în modelul Alhambra

Nu se stie exact cum ghidat de maeștrii arabi, dar este posibil ca acesta a fost similar cu metoda „Kira-Kira“. Cu această metodă, mai întâi cercul este împărțit în trei arce egale, atunci unul dintre ei este împărțit în trei părți, de fiecare dată când au folosit aceeași metodă care a fost utilizat expertul Toraja. Astfel, împărțim cercul în nouă arce egale, în timp ce laturile lor de strângere de coardă sunt nonagon corecte înscris în cercul inițial.

Comunicarea cu maestrii Toraja

Am ezitat să-i spun maeștrii Toraja că metoda „Kira-Kira“ pot fi aplicate cercului. Înainte de a se confrunta cu sarcina de a construi o stea cu cinci colțuri, comandantul folosit metoda sa de a face față cu orice alte probleme, dar aici a fost lipsit de putere. Mi-era teamă că, dacă i-am spus cum metoda utilizată poate fi extinsă de către același token-ul va indica maeștrilor faptul că arta lor nu este suficient de mare. Cu toate acestea, am decis că, după explicația mea, ei vor înțelege că ei înșiși au formulat o nouă sarcină, sunt dincolo de metoda lor.

Utilizarea funcțiilor trigonometrice speciale

Ce greșeală facem atunci când folosim o coardă a cercului ca valoare aproximativă a lungimii arcului său? Fie a și c - arc circumferința și coardă sale subîntinzând respectiv, r - raza cercului inițial, α - unghiul central de definire a arcului.

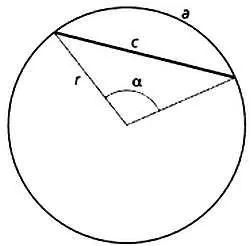
Prin urmare, funcția f (x) = sin (x) / x descrie raportul dintre coardă și arc circular contractabile ea. Astfel, ne-am arătat cum este posibil într-un nou mod de a utiliza această funcție trigonometrice neobișnuită, anterior de interes, în principal ca un exemplu de limită de calcul personalizat. În ciuda faptului că, atunci când x = 0, această funcție are un decalaj, limita funcției în acel moment, și există 1. Existența acestei limite este dovedită prin compararea cu arc și coardele cercului.

Atunci când o jumătate mai târziu, m-am întors în sat, comandantul a atras încă o stea cu cinci colțuri pe ochi. Când le-am spus cu privire la modul în care acestea pot schimba metoda lor și să-l utilizați pentru a împărți cercul în părți, au dat seama că am avut în minte, deja în curs de explicații, și a prezis rezultatul corect. Ei au acceptat metoda propusă și a început să folosească eu.

Cronica de experiențe matematice

Titlul original al cărții Davis și „Experiența matematică“ Hersh în limba engleză pare a fi matematică Experience. Experiența cuvânt are un sens mai larg decât cuvântul „experiență“ în limba română. Experiența - este atât experiența de viață și de experiență, care contribuie la formarea personalității. În același timp, experiența - este psihologic proces, personal. Astfel, numele Davis și cartea lui Hersh ar putea fi tradus ca „Experiența matematică“ - un proces care, pe de o parte, este personală, celălalt - dincolo de domeniul de aplicare al unui mediu de cultură și separat. El nu este limitat la lumea academică sau, dimpotrivă, numai viața de zi cu zi, poate fi tratată ca o teorie și practică, la cultura occidentală, precum și orice alte. Experiențele prezentate în acest capitol reflectă experiența matematică. Descris situația în afara domeniului de aplicare al unei singure culturi, ele combină știința și viața de zi cu zi, psihologice și personale, astfel încât acestea să poată fi într-adevăr numit un experiențe matematice.