mici mostre
Ca rezultat, experimente medicale si biologice, cercetatorii au obtinut date care sunt grupate în seriile statistice. Primul pas în studiul seriilor statistice este răspunsul la întrebarea, la ce tip de distribuție sunt rezultatele. În funcție de distribuția intenționat, se calculează caracteristicile de bază statistice: valori medii aritmetice (Așteptare), varianța, abaterea standard. Experimentul ideal este de a studia totalitatea tuturor obiectelor pentru a rezolva această problemă, și anume populația generală. De fapt, numărul de membri ai o astfel de combinație poate fi infinit, astfel încât în practică, studiind totalitatea selectivă a generalului. În acest caz, este necesar să se răspundă la întrebarea modului în care parametrii eșantionului se potrivesc cu populația generală, adică, calcularea parametrilor eșantionului special, pentru a evalua parametrii relevanți în populație. De exemplu, măsurarea creșterii studenților din primul curs din același grup, pentru a determina intervalul în care poate varia în creșterea tuturor studenților din primul an. Dacă luați câteva mostre (grupuri de studenți), apoi media aritmetică a probelor, cu numărul de membri din fiecare probă de 30 vor fi distribuite în jurul mediei generale a legii normale. La determinarea intervalului de încredere pentru media generală, în acest caz, este necesar să se utilizeze tabele statistice pentru probabilitatea normală integrală (tabelul 2 din anexă). În cazul în care numărul de membri din eșantion este mică (mai puțin de 30), există o îndoială cu privire la posibilitatea unor astfel de parametri de evaluare probe populația generală. Evaluarea modelelor de distribuție de aritmetică înseamnă probe cu un număr mic de observații făcute matematicianul englez Gosset (pseudonim Student). Distribuția de probabilitate rezultată a primit numele de T - distribuție Student. Luați în considerare pașii de bază de prelucrare a probei mici, utilizând distribuția Student. După cum acceptă denumiri: m - media aritmetică, D - variatie de (s 2), s - abaterea standard populația generală. s 2. s - corespunzătoare parametrilor de interogare.
Având în vedere un set de valori ale frecvenței cardiace (HR) la pacienții cu:
95 130 83 115 120
1. Găsiți valoarea mediei aritmetice a eșantionului înseamnă:
2. calcula varianța (seria de dispersie). La calcularea varianța unui mic eșantion suma pătratului abaterilor de fiecare dintre variantele de realizare ale mediei aritmetice valori nu se împarte volumul eșantionului n, iar numărul de n-1:
Numărul df = n-1 se numește numărul de grade de libertate. Semnificația acestui parametru în acest caz poate fi explicată după cum urmează: În cazul în care există o serie de variație constând din n membri, iar media aritmetică a fost determinată (), atunci fiecare valoare separată poate fi găsită prin cunoașterea și restul de n-1 variantă. Adică, există n-1 grade de libertate. În cazul în care numărul de ruleaza n este mai mare sau egală cu 30, diferența dintre n și n-1 nu este mare și nu afectează magnitudinea dispersiei.
3. Abaterea standard a eșantionului:
Am identificat așa-numitul punct (adică, exprimată printr-o singură valoare) parametrii unui mic eșantion. acum estimăm populația totală a eșantionului nostru.
4. Definiți valoarea medie a diferențelor dintre parametrii de eșantionare și populația generală. Această cantitate este numită eroarea pătratică medie (sau eroarea medie, o eroare de selecție eroare standard) sx:
Formula arată că dimensiunea definită de eroarea standard depinde de deviație standard s a probei și a probei dimensiune n. În cazul în care obiectele selectate în eșantion aleatoriu, cît este mai mare dimensiunea sa, este mai mică eroarea standard, și, prin urmare, mai puțin diferențele de personalizat și populația generală. Rezultatul este scris sub forma:
Pentru a determina intervalul de încredere cu un grad predeterminat de probabilitate, care este valoarea medie generală, introducem conceptul de criteriu deviere normalizat pentru distribuția t (Student lui t test):
Valoarea normalizată abatere t (Student ț) este valoarea diferenței dintre media aritmetică și proba medie generală m, exprimat în termeni de medie pătrată eroare.
Din formula (6), un interval de încredere pentru media generală va avea forma:
Sa constatat că valorile distribuției t este anormală, cu atât mai puternică n mai mică (Fig.1).
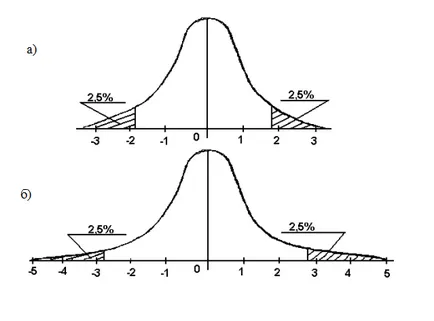
Fig.1. valori diferite ale t, de închidere de 2,5% din dreapta și
a) sub curba de distribuție normală (n =. t = 1,96),
b) în distribuție curba t-Student (n = 5, t = 2,78).
Prin urmare, probabilitatea de a găsi un eșantion înseamnă în anumite valori ale lui t este considerabil redusă în comparație cu distribuția normală. Astfel, pentru un nivel de încredere P = 0,95 tabele t valoare pentru distribuția normală este egală cu 1,96, și, prin urmare, intervalul de încredere:
Pentru n = numărul de experimente Tabelele 5 Student t = 2,78. Intervalul de încredere:
Prin creșterea n, t - t distributie aproape de normal. Când n 30, diferența aproape dispare între ele. testul t Student Mese construit pentru un anumit nivel de încredere (nivelul de semnificație) și numărul de grade de libertate: df = (n-1). De exemplu, pentru numărul de experimente n = 5 numărul de grade de libertate egal cu 4. La intersecția df = 4 și (nivel de semnificație - 0,05) P = 0,95, vom găsi testul t - 2,78 (tabelul 4, apendice).