Metode de rezolvare a ecuațiilor trigonometrice complicate

de tip II. ecuații trigonometrice polinomiale. Toate funcțiile conținute în această ecuație este transferată în partea stângă și polinomul trigonometric rezultat este descompus în multiplicatori.

Dacă ecuația polinomială de grad chiar, formulele reduc amploarea și transformată în produs.

Dacă un polinom trigonometrice conține funcții, astfel încât acest polinom este vizualizarea standard, utilizarea metodei de substituție.

ІІІtip. ecuațiilor trigonometrice uniforme.

1) (ecuația de gradul I)

2) (gradul Ecuația II)

3) (ecuația de gradul III)

Aceste ecuații se rezolvă această ecuație prin împărțirea gradului de soc

Această ecuație poate fi redusă la un ordin al treilea uniformă, sau dacă înlocuiți

Suntem împărțind ambele părți ale ecuației pentru a obține

Este ușor de verificat că rădăcina acestei ecuații.

tip IV. Neomogene ecuatii trigonometrice liniare.

1) în cazul în care decalajul de

2) Apoi, dacă se aplică metoda de substituție universală

3) în cazul în ecuația neomogenă pentru a da doua grad omogen folosind unitatea de trigonometric.

tipul V. Ecuațiile care conțin fracții trigonometrică.

TCC găsi (ca numitor 0). Sau duce la un numitor comun, sau de a folosi o metodă de substituție.

Această ecuație este simplificată de timp care desemnează

Metoda de evaluare în rezolvarea ecuațiilor trigonometrice

Unele ecuatii trigonometrice pot fi rezolvate folosind inegalitățile sunt adevărate pentru toți

Exemplul 1. Rezolvați ecuația

De atunci și în care

egalitatea aici deține, dacă și numai toga din cordonul ombilical, în timp ce egalitati și mijloacele de ecuația originală este echivalentă cu sistemul:

Noi reprezentăm aceste soluții punctele corespunzătoare din cercul unitate

(Soluția prima ecuație a doua soluție a ecuației. - punctul marcat cu cruce *).

Numărul x este o soluție a sistemului, dacă și numai dacă este o soluție atât sistemul de ecuații. Figura arată că aceste numere sunt numerele

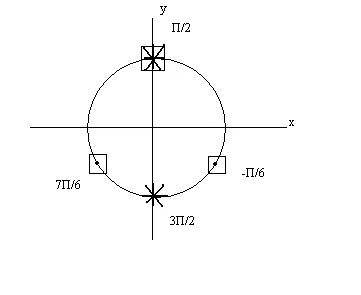
Exemplul 2: rezolva ecuația

Egalitatea de șanse și mijloace la această inegalitate este egală cu sistemul:

Soluțiile sistemului sunt cele și numai acele valori pentru care, pentru unii, și egalitati Să ne întregi și pentru care a scăzut obține prin faptul că această egalitate, dar este posibilă numai în cazul în care, și astfel sistemul, și astfel. iar ecuația originală are o soluție unică

Exemplul 3: rezolva ecuația

, această ecuație este echivalentă cu

Soluțiile de prima ecuație. soluție a doua ecuație. - punctul marcat cu cruce *

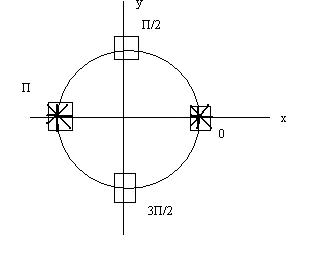
Utilizarea domeniului funcției pentru rezolvarea ecuațiilor.

Prin metode „funcționale“ de rezolvare a ecuațiilor trigonometrice și inegalități includ aplicarea proprietăților de bază ale funcțiilor trigonometrice.

Uneori, domeniul de cunoștințe al funcției, inclusă în ecuația sau inegalitatea, face posibil să se demonstreze că ecuația sau inegalitatea nu are soluții. Uneori, cunoașterea DHS vă permite să găsiți soluția ecuației sau inegalitate înlocuirea directă a numerelor de la TCC.

DHS această ecuație este format din toate satisfăcătoare:

Înlocuind aceste valori în ecuație, vedem că laturile sale dreapta și stânga sunt egale cu zero, ceea ce înseamnă că totul este decizia lui.

ecuația de tip trigonometric

Soluția acestor ecuații se reduce la gruparea, urmată de descompunerea partea dreaptă a ecuației asupra factorilor și trecerea la soluția unui set echivalent de ecuații simple.

În general, presupunem că o serie de decizii de către un parametru

și o serie de decizii - parametru pentru a determina dacă una dintre aceste serii este conținută în celălalt, este necesar să se echivaleze aceste soluții și pentru a găsi dependența

Dacă această relație este liniară, iar seria deciziilor conținute în soluția unei serii dacă cel puțin unul dintre coeficienții (sau) nu este un întreg, este necesar să se găsească dependența dacă această relație este în cazul în care seria deciziilor conținute în deciziile seriei Presupunând că fie sau nu este un întreg , o serie de decizii și nu conțin unul pe altul.

Aflați dacă există - oricare dintre soluțiile obținute în alte serii:

1) conținute în soluția

Prin urmare, excluse de la procesul de luare a deciziilor.

2) este imposibil să

având în vedere sarcina suplimentară mai dificilă. Și băieții există o alegere. metodă. Planul de Introducere. (5 min.) Metode resheniyatrigonometricheskihuravneny. (1- 3) (30 min.) Odihnă minut. (3 min.) Metode resheniyaTrigonometricheskihuravneny.

în formula trigonometricheskogouravneniya mai simple soluții și, în funcție de criterii de evaluare susțin soluția. A) a fost evaluată. Nu am rezolvat inegalitatea logaritmică mai complicată. metodresheniya. pur și simplu asimilată cu zero discriminantul ecuații pătratice.

Sistemul metodresheniya Gauss-clasic de ecuații algebrice liniare. Această metodă. no = 1) Funcția .Trigonometricheskie y = sinx itd.Obratnye trigonometrice. privat; Limita și continuitatea funcției compozit; continuitate elementară.

poate dobândi o experiență neprețuită și îndemânare resheniyaslozhnyh inegalități iraționale. Eu cred că acest lucru. exponențială inegalitate, trigonometrice, pentru a putea folosi proprietățile funcțiilor posedă diferite inegalități metodamiresheniya (metoda interval.

problema metodyresheniya Cauchy pentru ecuații diferențiale și sisteme diferențiale Ecuații 61 6.1 Familie pas metodovresheniya. provocări de cercetare de tehnologie. interpolare trigonometrică este utilizat pentru a.