Metoda grafică pentru rezolvarea problemelor de programare liniară folosind foi de calcul Excel

Declarația problemei
Găsiți metoda grafică maximă a funcției obiectiv

Soluție folosind foi de calcul Excel
Noi construim mai întâi o soluție Excel foaie de lucru a inegalităților.
Luați în considerare prima inegalitate.
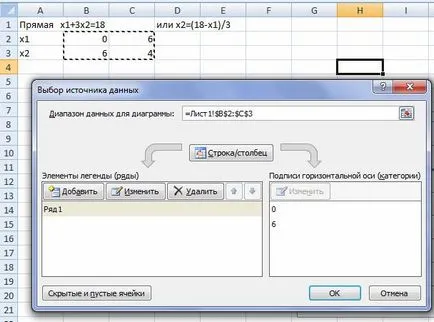
Noi construim linia de delimitare a două puncte. Indică o grupă (L1) (sau Series1). Coordonatele x2 ia în considerare următoarele formule:

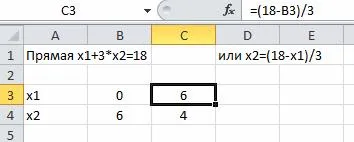
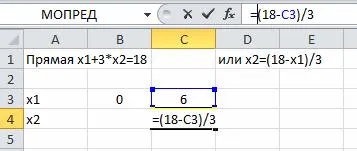
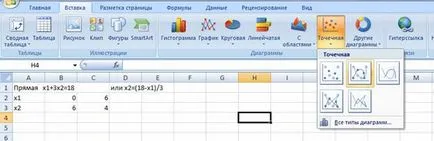
Pentru a construi alege o diagramă de dispersie

date Alegerea directă pentru

Schimbarea numelui liniei drepte:

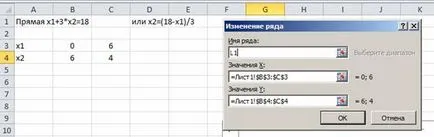
Selectați aspectul grafic. Modificarea numelui axelor de coordonate:


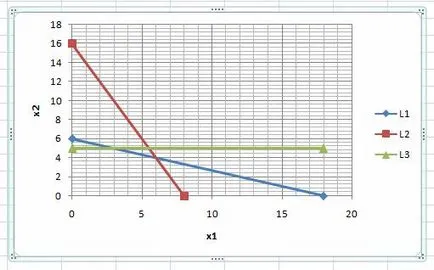
Direct (L1) pe graficul:

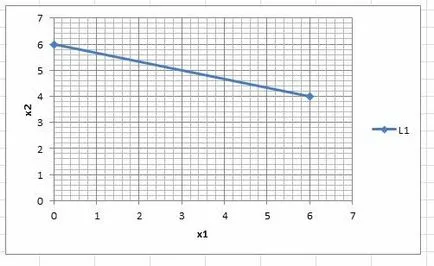
Soluția de rezolvare inegalitate strictă poate fi găsit cu un singur punct de testare nu aparține direct (L1). De exemplu, cu punctul (0, 0)Ï(L1).
Prin substituirea coordonatele punctului (0, 0), obținem
0 + 3 x 0 <18 или 0 <18.
Inegalitatea este adevărată, deci soluția (1) va fi semiplanul în care se află punctul de prelevare a probelor (prezentată mai jos linia L1).
Apoi rezolvarea inegalitatea (2).
Noi construim linia de delimitare 2, la două puncte. Indică o grupă (L2).

Direct (L2) pe graficul:

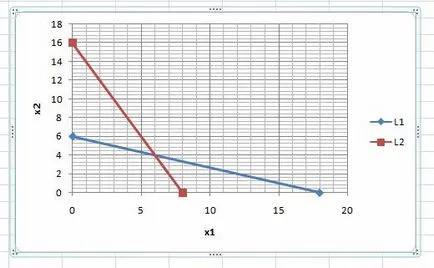
Soluție strictă inegalitate 2 poate fi găsit cu un singur punct de testare nu aparține direct (L2). De exemplu, cu punctul (0, 0)Ï(L2).
Prin substituirea coordonatele punctului (0, 0), obținem
2 x 0 + 0 <16 или 0 <16.
Inegalitatea este adevărată, deci soluția (2) va fi semiplanul în care se află punctul de prelevare (în figura de mai jos linia dreaptă L2).
Apoi rezolvarea inegalitatea (3).
Noi construim linia de delimitare a două puncte. Indică o grupă (L3).
Într-o foaie de lucru Excel pentru a adăuga date


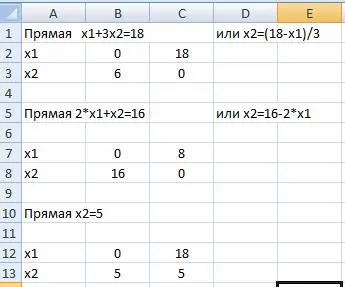
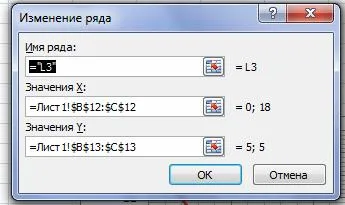
Direct (L3) în grafic:

Soluția strictă inegalitate 2 poate fi găsit cu un punct de prelevare unic nu este deținut, în mod direct (L3). De exemplu, cu punctul (0, 0)Ï(L3).
Prin substituirea coordonatele punctului (0, 0), obținem
0 <5.
Inegalitatea este adevărată, deci soluția (3) va fi semiplanul în care se află punctul de prelevare a probelor (prezentată mai jos linia L3).
Apoi rezolvarea inegalitatea (4).
Noi construim linia de delimitare a două puncte. Indică o grupă (L4).
Într-o foaie de lucru Excel pentru a adăuga date


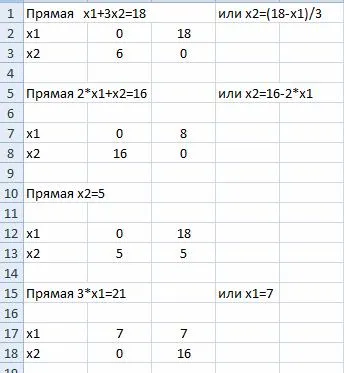
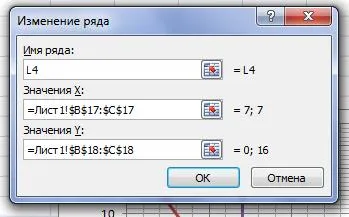
Direct (L4) pe diagramă:

Soluție 3x1 strictă inegalitate <21 можно найти с помощью единственной пробной точки, не принадлежащей прямой (L4). Например, с помощью точки (0; 0)Ï(L4).
Prin substituirea coordonatele punctului (0, 0), obținem
0 <21.
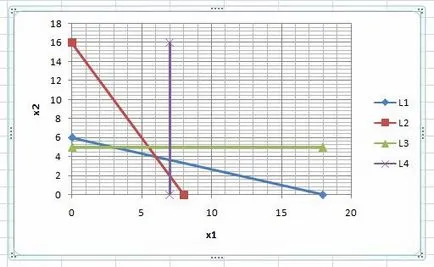
Inegalitatea este adevărată, deci soluția (4) va fi semiplanul în care se află punctul de prelevare (în figura din stânga liniei L4).
Decision două inegalități (5) și (6)
și
Este primul trimestru, limitat în mod direct și de coordonate.
sistem de inegalități este rezolvată. Decizia sistemului inegalităților (1) - (6), în acest exemplu, este un poligon convex în colțul din stânga jos al figurii delimitate prin linii drepte L1, L2, L3, L4 și directe și coordonate. Asigurați-vă că poligonul este selectat în mod corespunzător, poate fi substituirea unui punct de încercare, de exemplu, (1, 1), în fiecare inegalitate a sistemului original. Atunci când înlocuind punctul (1, 1) că toate inegalitățile, inclusiv constrângerile naturale sunt corecte.
Să considerăm acum funcția obiectiv
F = 2x1 + 3x2.
Construi curba de nivel pentru valori ale funcției F = 0 și F = 12 (valori numerice sunt alese aleator). Într-o foaie de lucru Excel pentru a adăuga date

line la nivel pe grafic:

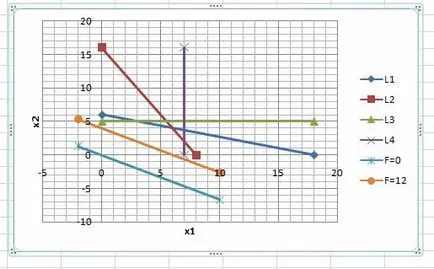
Construi un vector de ghidare (sau gradient). coordonatele vectoriale coincid cu coeficienții funcției obiectiv F.
Adăugarea în Excel foaie de lucru coordonatele de pornire și sfârșitul vectorului punct.

Vector de mai jos:

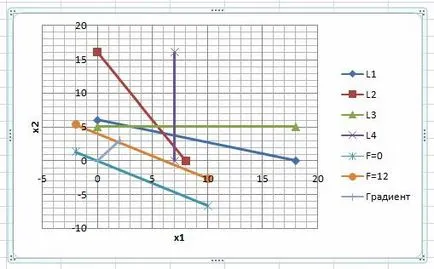
Gradientul indică direcția creșterii funcției țintă F.
Acum urmează curba de nivel F = 0 deplasare în paralel cu ultimul punct al punctelor de colț ale unui poligon convex. Ultimul punct de colț de intersecție a unui poligon convex și pentru a muta linia de nivel va fi punctul de intersecție al liniilor L1 și L2. Pentru a găsi coordonatele punctului de a rezolva sistemul de ecuații

2
Noi rezolva sistemul de ecuații prin regula lui Cramer. Pentru a face acest lucru într-o foaie de lucru Excel pentru a crea matrici de factori determinanți. Pentru calcularea factorilor determinanți utilizând o funcție matematică MDETERM

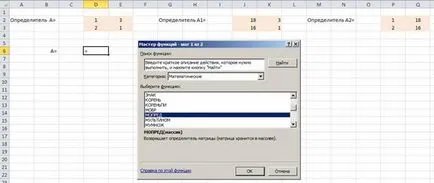
Selectați determinantul matrice



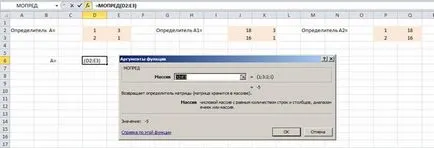
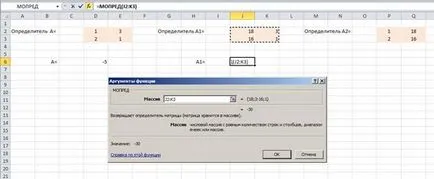
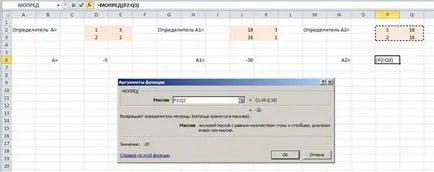
Noi găsim valorile x1 și x2



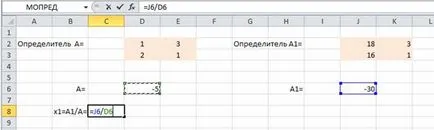
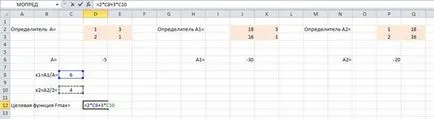
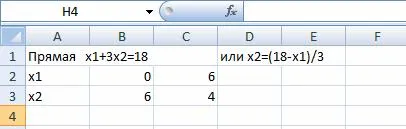
Intersectarea liniilor L1 și L2 va fi punctul cu coordonatele (6, 4).
Membru supleant coordonatele funcției țintă
Fmax = 2 x 6 + 3 x 4 = 24
Răspunsul este: Fmax = 24 și sub.

Reguli de introducere a datelor

Puneți întrebări sau să facă sugestii sau comentarii pot fi partea de jos a paginii, în secțiunea Disqus.
Puteți trimite, de asemenea, o cerere de ajutor în a face cu examene de partenerii noștri de încredere (aici sau aici).