matrice echivalentă de transformare primară și

Transformarea elementară pe rândurile de matrici se numesc rânduri următoarele transformări:

1. multiplicarea rând printr-un număr întreg non-zero;

2. Rearanjarea a două linii;

3. Adăugarea un rând de alte linii, înmulțit cu un număr diferit de zero.

Dacă matricea unei matrice de incrucisate folosind transformare echivalente pe rândurile, matricile sunt echivalente și reprezintă.

Exemple de transformări elementare,

Demonstrarea toate matricele elementare converti exemplul

Inmultiti primul rând al matricei în două, adică, fiecare element al primului rând este înmulțită cu doi, obținem o matrice rezultat. echivalent cu o matrice dată:

Schimbarea prima și a doua rânduri ale matricei, obținem o matrice echivalentă:

Din primul rând al matricei scade a doua linie, vom obține matricea echivalentă:

Ca rezultat, am ajuns la concluzia că matricea și echivalentul ca unuia dintre ei sa dus la celălalt prin intermediul unor transformări echivalente pe rânduri.

Kronecker - Capelli

Sistemul de ecuații liniare este consistentă dacă și numai dacă rangul matricei sale principale este egal cu rangul de matricea sa augmented, cu sistemul are o soluție unică dacă rangul este egal cu numărul de necunoscute, și un număr infinit de soluții, în cazul în care gradul este mai mic decât numărul de necunoscute.

Numere complexe. Adăugarea și multiplicarea

Complex [1] (număr imaginar învechit [2].) - numărul de specii. în cazul în care - numere reale - unitatea imaginară (valoarea pentru care egalitatea :). Setul tuturor numerelor complexe cu operații aritmetice este un domeniu și este de obicei notată cu limba latină. complexe - sunt strâns legate.

Aceasta înseamnă că (două numere complexe sunt egale dacă și numai dacă acestea sunt părțile reale și imaginare).

25) În cazul în care. atunci numărul este numit un complex conjugat al numărului.

Adică, complexul numerele conjugatuiui partea reală sunt egale și diferite semnul imaginar.

De exemplu. Conjugata complexă a numărului este numărul.

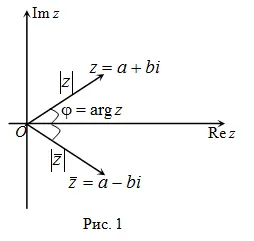
Pe plan complex de numere complexe conjugate obținute imagini în oglindă unul față de altul în raport cu axa reală.

Proprietățile numerelor complexe conjugate

1) În cazul în care. se poate concluziona că numărul considerat valid.

2) Pentru orice sumă număr complex - numărul real.

De exemplu. Să. atunci. și apoi

3) Pentru un produs complex număr arbitrar.

De exemplu. Să. numere de complex conjugat. atunci produsul

4) Modulele de numere complexe conjugate sunt egale. iar argumentele sunt semn diferit (Fig. 1).

9) În cazul în care - numere de complex conjugat, atunci