Math umaniste fără speranță

Derulam pentru Cheshire Cat și căderea în spațiul multidimensional.

vă prezentăm la următoarea lecție de la un profesor de matematica aplicata Nelly Litvak, care, împreună cu jurnalistul Alla Kechedzhan a decis să reabiliteze speriat matematica școală în umaniste. Pentru a face acest lucru, Nelly și Alla a organizat un grup pe Facebook pentru toata lumea „Matematica - mare și înfricoșată.“

Site-ul Newtonew Nelly fiecare material săptămână împărțit trecut la grup. Aici sunt link-uri la lecții anterioare, astfel încât să nu pierdeți nimic:

Uraaa, integralele terminat! Noi ne asigurăm că teorema lui Pitagora ne permite să se calculeze distanța nu numai într-o linie dreaptă, ci o curbă.

Ce se întâmplă dacă nu suntem în avion și în spațiul tridimensional? La urma urmei, lumea noastră nu este plat, ca tri-dimensională!

O distanță într-o linie dreaptă în spațiu tridimensional poate fi calculată din nou pe teorema lui Pitagora. Să încercăm să o facă.

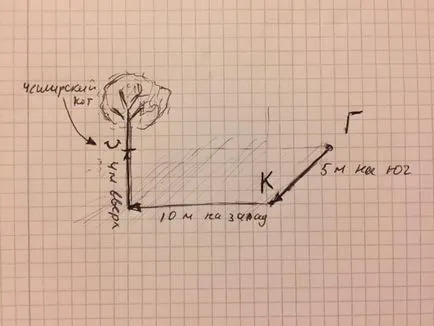
JOB. Cheshire Cat fuge de ducesei (T). El a condus la 5 metri la sud. Dar pe drum trunchiate regina (K) și este pe cale să strige: „Jos cu capul lui“ Sly Cat ducked și a fugit la vest, la 10 metri la cel mai apropiat copac. Pisica din lemn a urcat pana la 4 metri.

ÎNTREBARE: Care este distanța (în metri) în linie dreaptă, de la Ducesa Kota? (Pentru că acest lucru este Cheshire Cat, el, desigur, au dispărut, un zâmbet lăsat în figură).

CEL MAI IMPORTANT: Este doar un răspuns suficient. Explicați în mod necesar ca crezut!

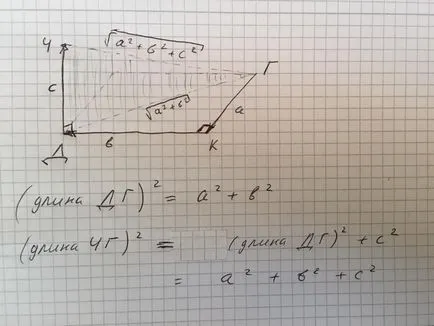
două triunghiuri pentru a vedea: 1 - "culcat" GCD (Duchess - Regina - Wood), și 2 - "stand-up" GDCH (Ducesa - Wood - Cheshire Cat). Dacă reușești, atunci este clar că DG picior - este ipotenuza primul triunghi situată GCD. Cunoscând lungimea celor două picioare ale PM și Duma de Stat, în conformitate cu teorema lui Pitagora, vom găsi lungimea ipotenuzei SM. Singura problemă este lungimea piciorului-ipotenuzei DG. DG = rădăcina sumei pătratelor 5 și 10 = 25 + 100 = A (care nu au egal amintesc că 2 ^ 11 = 121, atunci GD este de 11 m și Troshka cm). Acum MS. Această rădăcină de (16 + GD ^ 2) = SQRT (16+ (5 ^ 2 + 10 ^ 2)) = 11.87434209.

Între copac și unghiul la sol este, evident, o linie dreaptă. Unul dintre picior - distanța de la baza copacului Kota - 4 metri, al doilea - de la baza copacului reginei - 10 metri. Prin urmare, prin teorema lui Pitagora ipotenuza de lungime - distanța de la Kota la spugnuvshey regina lui. Noi credem: sqrt (4 ^ 2 + 10 ^ 2) = sqrt116. Acum știm două piciorul într-un alt triunghi dreptunghic în care ipotenuza - care este distanța dintre Ducesă și Cat într-o linie dreaptă. Unul dintre picior - aceasta este prima pisica martie, de la amanta sa la 5 metri de Sud, al doilea - distanța dintre Regina și pisica, pe care tocmai l-am calculat: sqrt (116 + 5 ^ 2) = 11, 87

De ce este important să se cunoască direcția de deplasare a pisicii - mai întâi spre sud, apoi spre vest? Pentru a nu pierde în spațiul de unghi drept!

Apropo, unii traducători Carroll a fost convins că este o pisica Cheshire. În limba engleză și, de fapt pisica, si pisica - doar o „pisica“.

Planul orizontal al traiectoriei rulajului pisica - picioarele unui triunghi dreptunghic. O linie dreaptă de la D la baza arborelui - este ipotenuza acea teorema lui Pitagora de neuitat: rădăcina pătrată a ^ 2 + 5 10 ^ 2 = 125. Rădăcina pătrată din 125 este de 11,2. Vertical (lemn) cat transportat cu avionul la 4 m. Și această distanță verticală cu lungimea detectată a ipotenuza se aseamănă din nou picioarele unui triunghi dreptunghic, lungimea ipotenuzei, care este distanța dorită. ^ 2 + 4 11,2 ^ 2 = 16 + 125 = 141. Rădăcina pătrată din 141 este de 11,9. Raspuns: 11,9 m.

In figura 2, sarcina într-o formă mai schematică. Distanța indicată în sud, vest și până literele a. b. c. Un punct este încă T (Duchess), K (Queen), D (piciorul copacului) și B (Cheshire Cat).

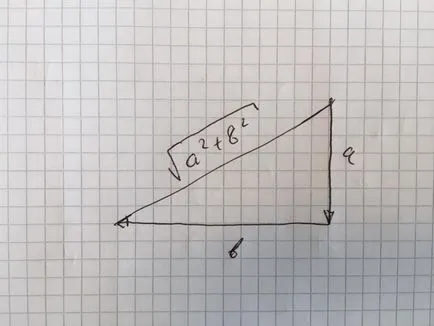
Dacă te duci cu avionul și metri la sud și vest b, distanța în linie dreaptă este sqrt (a ^ 2 + b ^ 2) de teorema lui Pitagora, vezi Fig. 3. Se pare că, dacă adăugați o treime coordonate și să treacă un metru în sus, formula este foarte similar, a crescut doar a treia dimensiune, iar distanța a fost sqrt (a ^ 2 + b ^ 2 + c ^ 2).

Unii participanți nu au fost luate în considerare de teorema lui Pitagora, și se uită pe internet. Dacă te duci la link-ul. veți vedea că această distanță este măsurată în așa-numitul spațiu „euclidiene“.

spațiu euclidian - aceasta este cea mai comună spațiul pe care îl vedem în jurul nostru. Distanța în acest spațiu, înțelegem „rezultatul Rigla pentru măsurarea.“ Și această distanță este calculată folosind teorema lui Pitagora.

Ultima sarcină a unei lungi serii despre teorema lui Pitagora. La sfârșitul privire la spațiul multidimensional. spațiu multi-dimensional al imaginației, cel puțin, deoarece acestea sunt aproape imposibil de imaginat! Creierul nostru nu știe cum să atragă o imagine cu patru dimensiuni, și numai aproximativ stomernyh sau TEN- și nu spun nimic.

Dar atunci de ce au nevoie? Se pare că spațiul multidimensional este foarte real! Pentru a începe cu, imaginați-vă că dorim să scrie o funcție, așa cum se arată în figura 4. coeficienții a. b. c. d poate fi orice număr, adică, avem patru „grade de libertate“. Se pare că astfel de funcții, așa cum se arată în Figura 4, „live“ în spațiu cu patru dimensiuni.

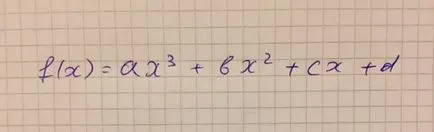
spațiu multi-dimensional sunt obținute, atunci când descriem un obiect cu ajutorul mai multor parametri. De exemplu: vârsta, înălțimea, greutatea, temperatura corpului. În al doilea rând, suntem în spațiu cu patru dimensiuni!

lumi moderne online este doar plin cu spații dimensiuni înfricoșătoare.

Și parametrii de utilizatori chiar mai mult: numărul de vizite la fiecare site, evaluarea fiecărui element, fiecare interogare de căutare. există milioane de opțiuni. Nu este o coincidență una dintre principalele sarcini de calcul în sistemele de recomandare on-line - este de a reduce dimensiunile.

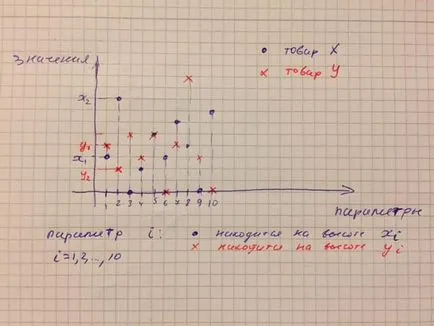
JOB. magazin online vinde produse. Pentru simplificare, să presupunem că mărfurile 10 parametri.

In figura 5, axa orizontală - numărul parametrului. Pe axa verticală - valoarea mărfurilor. Avem 2 produs: X (cercuri albastre) și V (cruci roșii). Valorile parametrului 1.2. 10 pentru produsul X va fi notat x1, x2. x10. și pentru mărfurile din SUA, respectiv, U1. v2. U10.

Dorim să oferim clienților produse care sunt „similare“ celor care le-au cumparat deja. Cum de a face acest lucru?

ÎNTREBARE: Au cum să numere „distanța“ dintre cele două produse. Este necesar ca distanța dintre „foarte diferite“ bunuri a fost ridicat, dar între produse „similare“ - mici.