Magic Box - soluții încrucișate sumă exemple cutii magice, numerele magice

Piața - un dreptunghi în cazul în care toate părțile sunt egale. Și în cazul în care părțile nu sunt egale, atunci, de rupere dreptunghi în celule pătrat, obținem un număr diferit de celule din rândul și coloana. În acest caz, este imposibil să se obțină cantități egale pe toate rânduri și coloane simultan. Relaxați-vă cerințele, va fi numit dreptunghiul magică în cazul în care suma numerelor de pe toate liniile sunt egale și separate, sumă egală cu numerele de pe toate coloanele, de exemplu, în dreptunghiul va fi de două sume magice, una pentru rânduri și unul pentru coloane.

Call - apel, și îl putem construi?

Să începem cu un dreptunghi 2x3 (liniile 2, 3 coloane). Suma de 2 + 1 + 3 + 4 + 5 + 6 = 21. divizibilă cu 3, dar nu este divizibil cu 2, ceea ce înseamnă că aceste numere nu pot fi repartizate pe două linii, astfel încât suma numerelor a fost același.

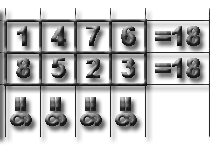
Vom continua căutarea. 2x4 dreptunghi ar trebui să conțină numerele de la 1 la 8. Suma de 1 + 2 +. + 8 = 36. și împărțit la numărul de linii și numărul de coloane. Descompunând numerele de pe o pereche de aceeași valoare, se obține cu ușurință 2x4 dreptunghiul magică. Este posibil să se tragă primele concluzii. O condiție necesară a existenței sale - suma numerelor pentru a aranja să fie împărțită și numărul de linii și numărul de coloane.

În plus, raportul dintre sumele liniilor și cantitățile relative ale posturilor este egal cu numărul de coloane copci. Să ne întoarcem la dimensiunea de 3x4. 5 = 1 +2+. + 12 = 78 nu este divizibil cu 4, vom zbura fără oprire la dimensiunea de 3x5. 1 + 2 +. + 15 = 120. divizibil cu 3, și 5, un dreptunghi posibil.

Am pus problema într-un mod general. Numerele de la 1 nk necesară pentru a plasa în dreptunghiul n rânduri și k coloane, astfel încât să formeze două cantități magice: S1 = (1 + nk) k / 2 pentru fiecare linie și S2 = (l + nk) n / 2 pentru fiecare coloană atunci dreptunghiului va fi numit magic. O condiție necesară pentru construirea unui astfel de dreptunghi găsit, a demonstrat existența a două exemple, continuați la vârful degetelor.