M-2 Overbeck pendul

rotație studiu Fa prin cruciat Overbeck pendul

Scopul este de a studia legile de mișcare de rotație pentru a determina momentul de inerție J Oberbeck pendul.

2 Echipamente și Consumabile

Overbeck pendul, cronometru, set de bunuri.

3 Partea teoretică

3.1 Definiții și legi ale dinamicii mișcării de rotație de bază

InertsiiJ impuls unui punct de masă m de material în raport cu axa de rotație este definită ca fiind egală cu produsul dintre punctele de masă pe pătratul distanței față de axa sa în considerare:

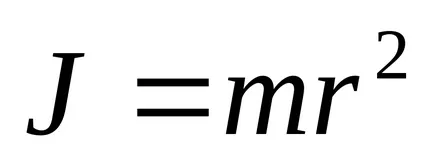
Momentul de inerție al sistemului de puncte (corpului) în raport cu axa de rotație se numește mărimea fizică egală cu cantitatea în greutate n bucăți de puncte materiale ale sistemului prin pătratul distanței lor față de axa considerată:

În cazul unei distribuții continue a masei, această sumă este redusă la integralei

, în cazul în care integrarea se realizează pe întregul volum al corpului. Velichinar în acest caz, este o funcție a poziției punctului cu coordonate x. y. z.

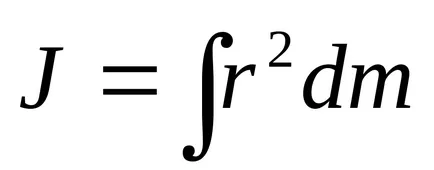
Dacă un moment cunoscut de inerție Jc a corpului în jurul unei axe care trece prin centrul de masă, momentul de inerție J în raport reciproc paralele cu axa definită de teorema lui Steiner.

Steiner teoremă. J momentul de inerție în jurul oricărei axe de rotație egală cu momentul de inerție Jc în raport cu axa sa de paralele care trec prin centrul de greutate corporală C, cu produsul pliat asupra greutății corporale și pătratul distanței dintre axe:

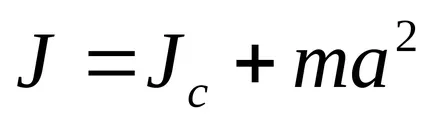
moment de forță

în raport cu un punct fix G se numește o valoare fizică determinată de produsul vectorial al vectorului rază

, trase din punctul O la punctul A de aplicare a forței asupra forței

. vectorul

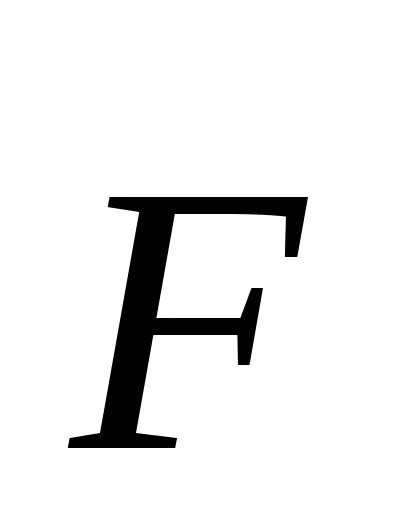
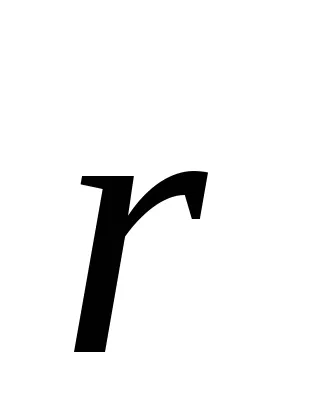
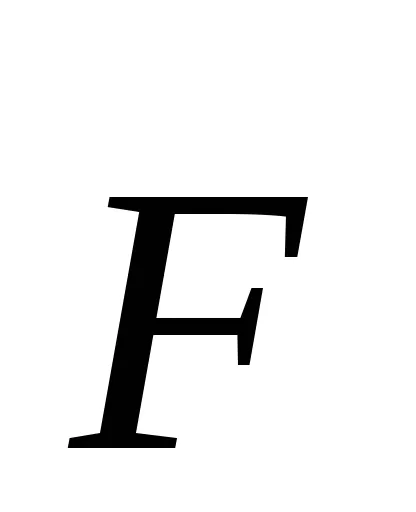
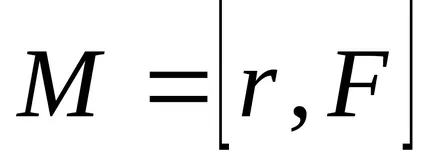
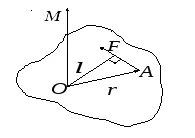
Figura 1 - Cuplu

- pseudo direcția sa determinat prin regula șurubului din dreapta (figura 1).

Forța cuplului modulului

Aici α - unghiul dintre

și

, r = sinα l - cea mai scurtă distanță dintre linia de acțiune a forței și axa de rotație se numește forța umerilor.

Ecuația fundamentală a dinamicii de rotație a mișcării a corpului rigid în raport cu o axă fixă: suma momentelor forțelor care acționează asupra corpului în jurul unei axe, este produsul a momentului de inerție al corpului în raport cu aceeași accelerație unghiulară axă, corpul dobândit

în formă vectorială

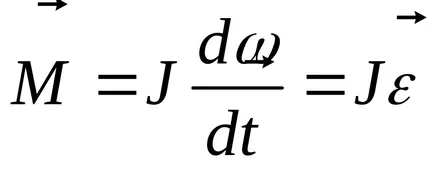
impuls unghiular

Un punct material în raport cu punctul O fix se numește cantitatea fizică determinată de produsul vectorial:

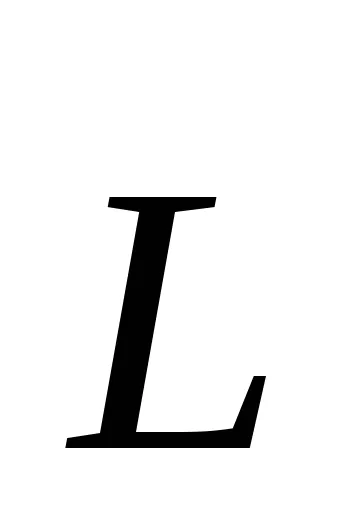
unde

- vector raza de la punctul O la punctul A;

- impuls unui punct material.

- pseudo direcția sa determinat prin regula șurubului dreptaci.

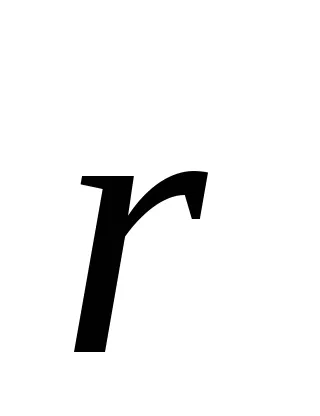
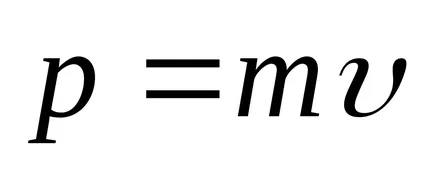
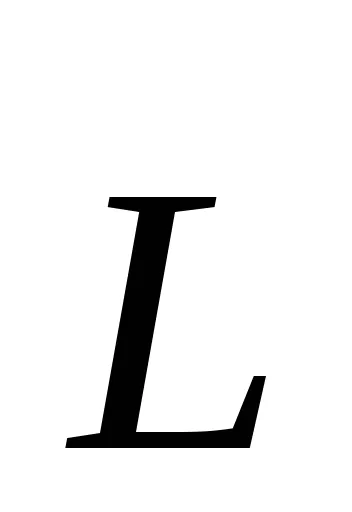
Să considerăm un corp rigid rotativ în jurul unei axe fixe. diviza Mental corpul în volume mici de mase elementare mi. la ri distanță de axa de rotație. La rotație, aceste volume vor avea diferite viteze liniare

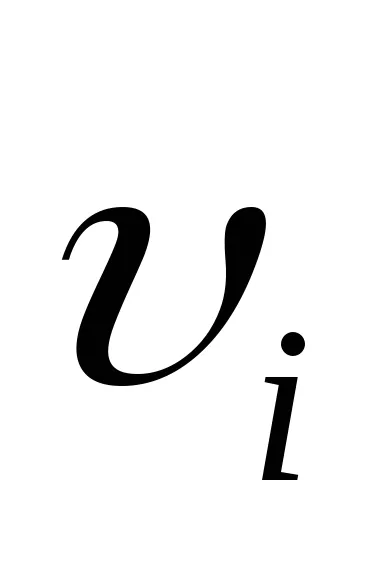
Moment de impuls corpului solid in jurul axei este egală cu suma momentului cinetic particulelor individuale:

viteza de translatie

Acesta este asociat cu o viteză unghiulară ω prin următoarea relație:

. Astfel, pentru o viteză unghiulară corp perfect rigid al particulelor care constituie este același.

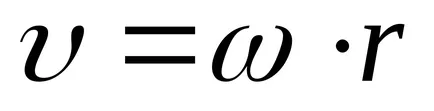
Cu aceasta în minte, folosind (1), scrie (4) în formă.

astfel momentul solid de impuls în jurul axei corpului este egală cu produsul dintre momentul de inerție în raport cu aceeași axă la o viteză unghiulară a corpului

Diferențierea ecuația (5), în timp:

Ie ecuația fundamentală a dinamicii mișcării de rotație a corpului rigid în raport cu axa fixă (3) poate fi scrisă ca:

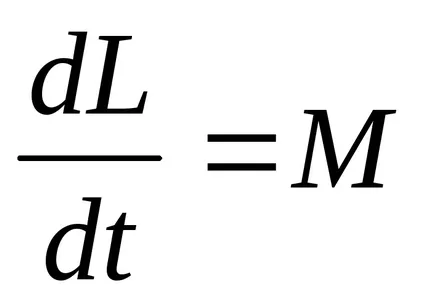
- timpul de pulsații derivat corp rigid în raport cu axa de rotație egală cu forțele momentului în jurul aceleiași axe.

În formă vectorială

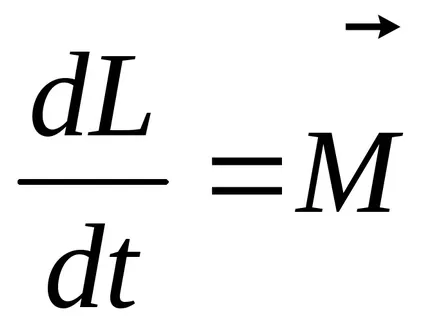
Într-un sistem închis în momentul forțelor externe

și

, de unde

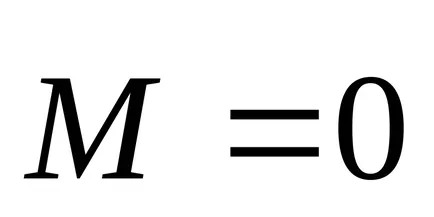
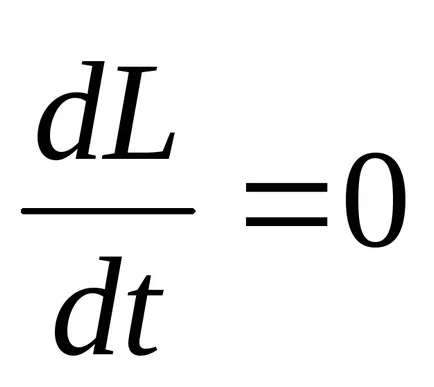
- această expresie este legea conservării momentului cinetic.

Legea conservării momentului cinetic. impuls unui sistem închis este conservată, adică Ea nu se modifică în timp.

Figura 2 - Experiența cu Zhukovsky banc

Pentru a demonstra conservarea momentului cinetic poate fi prin intermediul Zhukovskogo banc (Figura 2). O persoană care stă pe banca, care se rotesc în jurul unei fără fricțiuni axă verticală, care deține greutățile în mâini și se rotește cu o viteză unghiulară ω1. Dacă un om lăsă mâinile în jos, momentul de inerție este redusă, crescând astfel w2 viteza unghiulară a rotației sale. Legea conservării momentului cinetic pentru această experiență: J1ω1 = J2ω2.

3.2 Descrierea configurării experimentale

Overbeck pendul (Figura 3) este format din patru spițe 1 fixate pe manșonul 2 în unghi drept una față de alta. Pe aceeași manșonul nasazhany două role de 3 și 4 din diferite raze (r1 și r2). Întregul sistem este liber să se rotească în jurul unei axe orizontale. Momentul de inerție al pendulului Oberbeck poate fi modificat prin deplasarea sarcinilor de-a lungul spițele 5. Forțele Moment create de sarcină 6 m. masa suspendat din filament 7, care este înfășurat pe una dintre scripeții și este aruncat prin blocul 8. Sub acțiunea sistemului de accelerare constantă a cuplului se va roti cu o  constantă accelerație unghiulară. În starea inactivă a pendulului este imobilizat din rotația elementului de fixare 9. Deplasarea sarcinii poate fi determinată pe scara verticală 10.

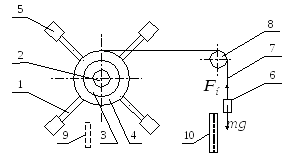
Figura 3 - Pendulul Oberbeck

Momentul de inerție J Oberbeck pendulului poate fi determinată teoretic ca sumă a momentelor de inerție ale pieselor în raport cu axa de rotație conform (1) sau experimental prin aplicarea conceptelor și legilor dinamicii mișcării de rotație.

Rotație Oberbeck pendul sub influența forței rezultante momentul M supune ecuația de bază a dinamicii mișcării de rotație (3).

Cargo m deplasează cu accelerație uniformă. Prin măsurarea timpului t. în care m marfă din repaus coboară printr-o distanță h. Puteți găsi accelerarea sarcinii:

accelerație unghiulară

. Dacă presupunem că firul nu aluneca pe marginea scripete, apoi accelerarea sarcina este egală cu accelerația de puncte de pe marginea rolei, și = r

= r

, de aici:

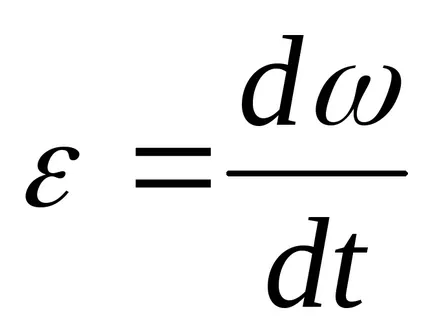
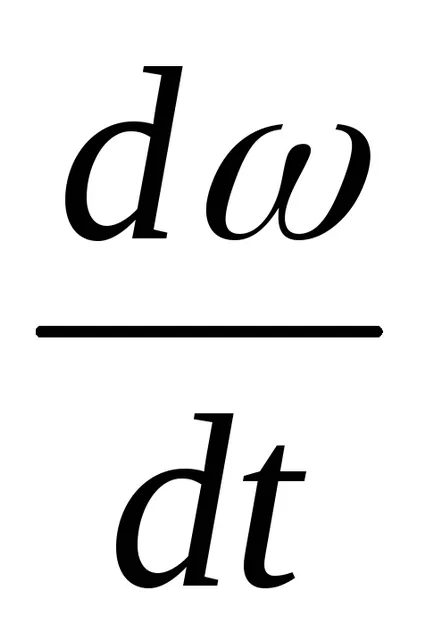
unde r - raza rolei.

Dacă prin fN denotă forța de tensionare a firului, cuplul potrivit tensiunii fire (2) este egal cu:

Forța FH poate fi găsit din ecuațiile de mișcare a sarcinii:

Cuplul de frecare Mtr tinde să fie destul de mare și poate denatura în mod semnificativ rezultatele experimentului. Prin urmare, (3) reprezintă momentul forței care acționează asupra pendulului Oberbeck ca momente ce rezultă tensiune fire și frecare:

Mtr MH- =

(13)

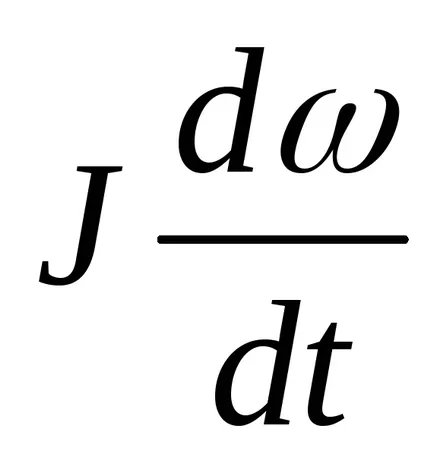
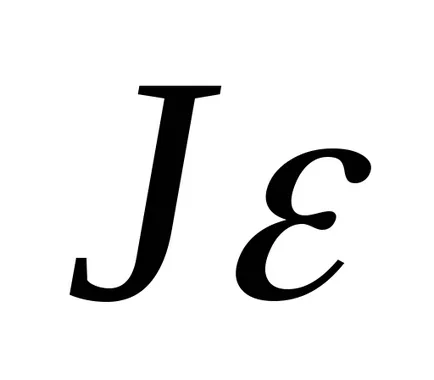
Dacă rotația este uniform accelerată și se supune ecuația (13), apoi grafic dependența accelerației unghiulare a cuplului care acționează asupra sistemului, va fi o linie dreaptă care trece prin punctul [Mtr; 0] (Figura 4). Factorul de proporționalitate este momentul de inerție necesar a pendulului Oberbeck:

Astfel, dacă este posibil, valorile experimentale pentru a construi un grafic al funcției

o linie oblică dreaptă, atunci putem vorbi despre respectarea ecuația fundamentală a dinamicii mișcării de rotație (3).

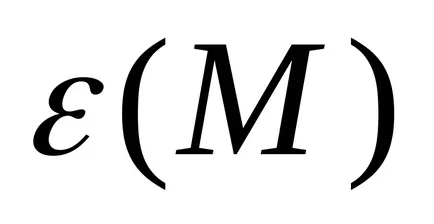
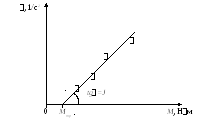
Figura 4 - Dependența accelerației unghiulare a cuplului care acționează asupra sistemului

Vă rugăm să rețineți că punctele experimentale din cauza efectului erorilor de măsurare și nu se poate afla pe o linie dreaptă. Prin urmare, este necesar să se efectueze o astfel de linie dreaptă medie, pentru care devierile puncte pe ambele părți sunt aproximativ aceleași. Direct nu traversează originea, deoarece sistemul funcționează cuplul de frecare. În cazul în care masa m este o greutate agățat pe un fir, este mică, sistemul poate rămâne în echilibru. Cu alte cuvinte, rotația pendulului va începe numai atunci când tensiunea MN de cuplu va fi mai frecare cuplu mtr.

4 Ordinea lucrărilor

Verificați parametrii sistemului indicate în tabelul 1.

Asigurați-vă că firul este înfășurat 7 de pe rola 4, cu creșterea razei și este r2 aruncat prin blocul 8 (figura 3).

Rotiți elementul de blocare 9 și să se asigure că pendulul este liber să se rotească în jurul unei axe orizontale.

Să consolideze pe m1 masa sarcinii firului și rotirea încet pendul, setați sarcina, astfel încât capătul său inferior a fost pe semnul „0“ pe scara verticală 10.

Folosind un cronometru, determina timpul t1. pentru care mărfurile vor cădea o distanță h. Stinge rotație pendul prin elementul de blocare. Respectați regulile de siguranță.

Se înregistrează valoarea t1 în tabelul 2.

Se repetă testul pentru acea sarcină de două ori mai mult, nota în tabelul 1, valorile T2. t3.

Repetați pașii 1-6 pentru masele de marfă m2. m3. m4. enumerate în tabelul 1, rezultatele măsurătorilor.

Aduce sistemul la starea inițială.

5 rezultate

Se calculează media aritmetică a timpului de deplasare a fiecărui transfer.

Pentru fiecare sarcină cu formula (8), determină accelerația a.

Se determină  accelerația unghiulară prin formula (9).

Luând accelerația gravitațională g egală cu 9,81 m / s 2, definesc forța de tensionare a firului fN (12) și momentul acestei forțe MH (10). Razele scripeților sunt prezentate în tabelul 1.

Conform valorilor calculate complot dependența

. Compara cu Figura 4. Faceti o concluzie cu privire la natura de rotație și de conformitate dinamica ecuațiile de mișcare de rotație (3).

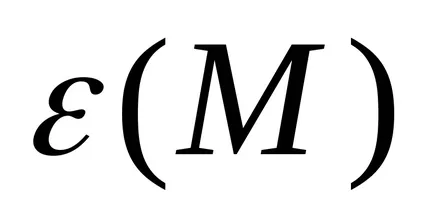
Prin reprezentarea grafică

determină valoarea cuplului de frecare Mtr. El se va întâlni punctul de intersecție al liniei drepte cu axa x. Înregistrați această valoare.

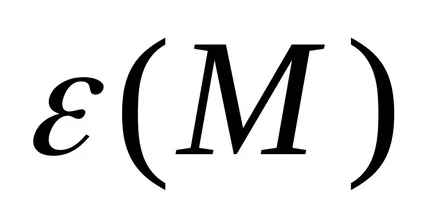
Prin formula (14) pentru a determina valoarea momentului de inerție J Oberbeck pendul. Completați tabelul de 2 măsurători.

Tabelul 1 - Setări sistem

Se determină valoarea medie a momentului de inerție al pendulului JSR Oberbeck.

Se determină erorile relative măsurători directe h. t și m. știind că valorile eroarea relativă X

Pentru cele mai mari max determina eroarea absolută

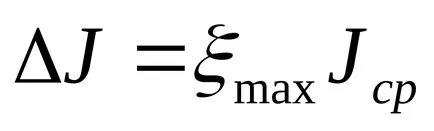
Imaginați-vă un răspuns în formă de

, kgm 2.

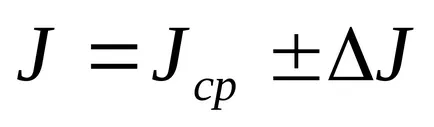
6 Lista de verificare

Ceea ce se numește momentul de inerție al punctului material al corpului (al unui sistem) în raport cu axa de rotație?

Ce determină momentul de inerție al pendulului Oberbeck în această lucrare?

Va momentul de inerție al pendulului Oberbeck în această lucrare la schimbarea razei rolei?

Ecuația fundamentală a dinamicii de rotație a corpului în jurul unei axe fixe.

Precizați legea conservării momentului cinetic. Dă exemple.

Rezolva elemente de testare de mai jos.

Trei minge mică situat la vârfurile unui triunghi echilateral. Momentul de inerție al sistemului în raport cu axa O1. perpendicular pe planul triunghiului și care trece prin centrul său - J1. Momentul de inerție al sistemului în raport cu axa O2. care trece printr-una dintre bilele - J2. Aserțiunea ...