Liniile și avioane în spațiu - studopediya

Ecuația liniei ca linia de intersecție a două planuri:

Prin fiecare linie în spațiul trece nenumărate avioane. Orice două dintre ele se intersectează și definiți-o în spațiu. Prin urmare, oricare două ecuații ale planurilor analizate împreună reprezintă ecuația acestei linii.

In general, oricare două planuri neparalele definite ecuațiile generale

Linia dreaptă de intersecție a acestora. Aceste ecuații sunt numite ecuația generală a liniei.

ecuația liniei care trece prin cele două puncte:

Dacă punctele de date A și B Minciuna pe o linie dreaptă paralelă cu axa Ox (y2 -U1 = 0) sau axa Ou (-h1 x2 = 0), atunci ecuația liniei va avea respectiv forma y = y1 și x = x1

Exemplul 4. Crearea ecuație a unei linii drepte care trece prin punctele A (1, 2) și B (-1, 1).

Soluție: Substituind în ecuația (8) x1 = 1, y1 = 2, x2 = -1; y2 = 1, obținem:
sau unde 2y = 4-x-1 sau x-2y în final + 3 = 0

Ecuația Canonical a liniei:

Să planul fix de coordonate cartezian rectangular sistem Oxy. Ne propunem sarcina: obține ecuația a liniei A. în cazul în care - un punct și o linie dreaptă - vectorul direcția unei linii drepte a.

Să - punct al liniei plutitoare. Apoi, vectorul este vectorul de direcție al unei linii drepte și are coordonatele (dacă este necesar, a se vedea coordonatele statyunahozhdenie ale coordonatelor punctelor). Evident, mulțimea tuturor punctelor de pe planul determinat linia dreaptă care trece prin punctul și având un vector de direcție dacă și numai dacă vectorii sunt coliniari.

Scriem condiția necesară și suficientă a colinearității vectorilor. . Ultima egalitate în formă de coordonate este.

În cazul în care. atunci putem scrie

Ecuația rezultată se numește forma canonică în ecuația planul liniei în dreptunghiular sistemul de coordonate Oxy. Ecuația este numită ecuația unei linii drepte în forma canonică.

Deci, ecuația canonică a liniei în seturile de vizualizare plane într-un sistem de coordonate rectangulare Oxy linie dreaptă care trece prin punctul și având un vector de direcție.

Aici este un exemplu de ecuația canonică a unei linii drepte în avion.

De exemplu, ecuația este ecuatia unei linii drepte în forma canonică. Linia care corespunde acestei ecuații trece prin punctul. și - vectorul direcție. Mai jos este o ilustrare grafică.

Notă următoarele fapte importante:

· Dacă - vectorul direcție al unei linii drepte și linia dreaptă trece prin punctul similar. și prin punctul. atunci ecuația canonică poate fi scrisă. și;

· Dacă - vectorul direcție al unei linii drepte, atunci fiecare dintre vectorii este, de asemenea, un vector de direcție a liniei drepte, prin urmare, oricare dintre ecuațiile unei linii drepte care corespunde unei forme canonice.

Ecuațiile parametrice ale liniei:

Teorema. Următorul sistem de ecuații este o ecuație parametrică a liniei:

unde - coordonatele unui punct fix al liniei, - coordonatele corespunzătoare ale unui vector de direcție arbitrară a liniei drepte, t - parametrul.

Dovada. În conformitate cu ecuația definiția oricărui set de puncte ale spațiului de coordonate, trebuie să arătăm că ecuațiile (7) satisfac toate punctele liniei L, și pe de altă parte, nu îndeplinește coordonatele unui punct care nu se află pe o linie dreaptă.

Să fie un punct arbitrar. Apoi vectorii și sunt coliniari, prin definiție și prin teorema colinearității a doi vectori, rezultă că o singură combinație liniară a celuilalt, adică, există un număr. asta. Din egalitatea vectorilor și egalitatea de origine a acestora:

În schimb, lăsați punctul. Apoi, prin teorema de pe colinearității vectorilor nici unul dintre ele nu poate fi exprimată liniar în termeni de altul, și anume, și cel puțin una din ecuațiile (7) nu este îndeplinită. Astfel, ecuațiile (7) udovletvoryayutkoordinaty numai acele puncte care se află pe linie dreaptă L, și numai acestea, QED

Ecuația normală a planului:

În formă vectorială, ecuația plan ia forma

Dacă vectorul normal al planului - o singură,

atunci ecuația planului poate fi scrisă ca

(Ecuația plane Normal).

- distanța de la origine la planul. . - a cosinus direcția de normale

unde - unghiul dintre planul normal și axele de coordonate, respectiv.

Ecuația generală a unui plan (8) pot fi aduse la multiplicarea normală cu un factor de normalizare. semna înainte de lovitura opusă elementului liber (8).

Distanța de la un punct la un plan (8) este situat într-o formulă obținută prin substituirea punctului în ecuația normală

Ecuația generală a planului, studiul ecuației generale a planului:

În cazul în care este dată spațiul tridimensional un sistem de coordonate rectangulare Oxyz. ecuația plan în acest sistem este un spațiu tridimensional de coordonate numită o ecuație cu trei necunoscutele x. y și z. care este îndeplinită de coordonatele punctelor în plan și nu a îndeplinit coordonatele oricărui alt punct. Cu alte cuvinte, prin substituirea coordonatele unui punct în ecuația plan al acestui plan obținem identitatea, iar atunci când este substituită în ecuația de coordonate plan la orice alt punct va egalitatea falsă.

Înainte de a scrie ecuația generală a planului, ne amintim definiția unei linii drepte perpendicular pe planul: perpendicular direct la planul în cazul în care este perpendicular pe orice linie dreaptă situată în planul. Din această definiție rezultă că orice plan perpendicular pe vectorul normal al oricărui vector nenul situată în planul. Acest fapt le folosim în dovada teorema următoare, care definește forma ecuației generale a planului.

Orice ecuație a formei. unde AB C și D - sunt numere reale, în care A, B și C nu sunt simultan la zero, definește un plan într-un dreptunghiular predeterminat sistemului de coordonate Oxyz în spațiul tridimensional, și fiecare plan în dreptunghiular sistem Oxyz de coordonate în spațiul tridimensional este definit de ecuația stabilită pentru unele numerele AB C și D.

Dupa cum se poate vedea, teorema este format din două părți. În prima parte, ni se dă ecuația și trebuie să dovedească faptul că acesta definește un plan. În a doua parte, ni se dă un avion și trebuie să demonstreze că este posibil să se determine o ecuație pentru o anumită gamă de numere AV C și D.

Să începem cu prima parte a demonstrației teoremei.

Deoarece numerele A, B și C nu sunt simultan egale cu zero, atunci există un punct. coordonatele cărora satisfac ecuația. adică, egalitatea. Scădeți laturile din stânga și din dreapta a acestei ecuații, respectiv, din stânga și din dreapta părți ale ecuației. astfel, obținem ecuația este echivalentă cu ecuația originală. Acum, dacă demonstrăm că ecuația definește un plan, se dovedește că ecuația echivalentă definește, de asemenea, un plan de la un sistem de coordonate rectangular predeterminat în spațiul tridimensional.

Egalitatea este o condiție necesară și suficientă a perpendicularității și vectori. Cu alte cuvinte, punctul flotant coordonatele satisfac ecuația și apoi numai când vectorii perpendiculare. Apoi, având în vedere faptul menționat anterior Teorema, putem spune că, dacă egalitatea. setul de puncte definește un plan care este vectorul normal. în care acest plan trece prin punctul. Cu alte cuvinte, ecuația definește un sistem koordinatOxyz dreptunghiular în spațiul tridimensional definit deasupra planului. Prin urmare, o ecuație echivalentă definește în același plan. Prima parte a teoremei.

Vom proceda la dovada celei de a doua parte.

Să presupunem că avem un plan care trece prin punctul. vector normal, care este. Vom dovedi că într-un sistem de coordonate rectangulare Oxyz stabilește ecuația formei.

Pentru a face acest lucru, vom lua un punct arbitrar al avionului. Să fie acest punct. Apoi vectorii sunt perpendiculare și, prin urmare, produsul lor scalar este zero :. După ce a luat. Ecuația devine. Această ecuație definește planul nostru. Astfel, teorema este complet demonstrată.

Ecuația se numește ecuația generală a unui plan, în sistemul de coordonate dreptunghiular Oxyz în spațiul tridimensional.

Ecuația generală a unei forme plane. în care: - un număr real altul decât zero, determină coordonate dreptunghiular sistem Oxyz plan care coincide cu planul. specifică, deoarece același set de trei-dimensionale de puncte în spațiu. De exemplu, ecuațiile și specificați același plan în care satisfac coordonatele același spațiu tridimensional de puncte.

Bit clarifica sensul teoremei.

Dreptunghiular predeterminat Sistemul de coordonate Oxyz planul și ecuația generală indisolubil legată. Aceasta înseamnă că fiecare plan corespunde ecuației planul general al formei (cu anumite valori ale numerelor A. B. C și D), iar această ecuație corespunde cu planul predeterminat dreptunghiular sistem de coordonate în spațiul tridimensional.

Iată un exemplu care arată ultima propoziție.

Uită-te la desenul planului în spațiul tridimensional, la un fix de coordonate rectangulare Oxyz sistem. Acest plan corespunde ecuației. deoarece este satisfăcută de coordonatele oricărui punct în plan. Pe de altă parte, ecuația definește un sistem de coordonate set Oxyz predeterminat de puncte a căror imagine este reprezentată în planul fig.

Ecuația a planului în bucăți:

Să presupunem că în spațiul tridimensional dreptunghiular specificat sistemul de coordonate Oxyz.

In carteziene sistemul de coordonate Oxyz în ecuația spațiul tridimensional al formei. în cazul în care un. b și c - nenule numere reale, numită ecuația planului în bucăți. Acest nume nu este intamplatoare. Valorile absolute ale numerelor a. b și c sunt lungimile segmentelor, plan care intersectează axele de coordonate Ox. Oy și Oz, respectiv, pornind de la origine. Numerele ecuson de. arată b și c în ce direcție (pozitive sau negative) sunt depuse la intervale axelor de coordonate. Într-adevăr, coordonatele punctelor satisfac ecuația planului în bucăți:

Uită-te la imagine, explicând acest punct.

Ecuația planului care trece prin punctul perpendicular pe vectorul: Să presupunem că în spațiul tridimensional este definit sistemul de coordonate cartezian rectangular. Să formuleze următoarea problemă:

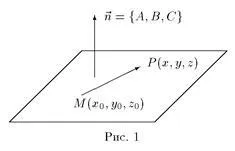
Scrierea ortogonalitatea vectorilor (. → n MP) = 0 formă coordonata, obținem:

Aceasta este ecuația dorită. Vector → n = A. B. C> se numește un vector normal al avionului.

Astfel, pentru a scrie ecuația planului, trebuie să știți vectorul normal al planului și orice avion punct prinazhdezhaschuyu.

Dacă acum în ecuația (1), pentru a deschide parantezele și ca rezultat termeni similari, obținem ecuația generală a planului:

Ecuația a planului care trece prin trei puncte:

Să presupunem că în spațiul tridimensional este fixat dreptunghiular sistem de coordonate Oxyz. conține trei puncte distincte. care nu se află pe o singură linie. A avut următoarea problemă: să scrie ecuația planului care trece prin aceste trei puncte.

Vom arăta două moduri de a rezolva problema.

Prima ecuații Metoda de compilare planul care trece prin cele trei puncte specificate.

Este cunoscut faptul că ecuația generală a seturilor de formă în plan dreptunghiular sistem de coordonate Oxyz plane. care trece prin punctul. și vectorul normal al planului are coordonatele. Prin urmare, putem obține o ecuație generală a planului, dacă știm coordonatele punctului prin care trece, și coordonatele vectorului normal al acestui plan. Din această cunoaștere și va construi atunci când ecuația unui plan care trece prin trei puncte date.

Deci, din condițiile problemei, cunoaștem coordonatele punctului (chiar și coordonatele trei puncte), prin care planul a cărui ecuație avem nevoie pentru a face. Rămâne de a găsi coordonatele vectorului normal al acestui plan.

Deoarece vectorul normal al planului și orice vector nenul perpendicular pe acest plan, vectorul perpendicular atât vectorul. și vectorul. În consecință, ca un vector, puteți lua produsul vectorial și. Deoarece u (vezi articolul prin calcularea coordonatelor vectorului coordonatelor punctelor, dacă este necesar), atunci. După calcularea determinantului înregistrat devin coordonate normale vector vizibile. și poate înregistra ecuația dorită a planului care trece prin cele trei puncte specificate.

A doua metodă de a găsi ecuația planului care trece prin cele trei puncte specificate.

Evident, punctele stabilite definește un sistem koordinatOxyz dreptunghiular în spațiul tridimensional, planul care trece prin trei diferite și nu se află pe un punct de linie dreaptă. dacă și numai dacă cei trei vectori și coplanară.

În consecință, în cazul în care starea de coplanaritate a trei vectori. adică, un produs mixt al vectorilor trebuie să fie zero :. Această ecuație în formă de coordonate este. Este, după calcularea determinantului este o ecuație generală a unui plan care trece prin cele trei puncte specificate.

Mai mult, din ecuația generală care rezultă dintr-un plan care trece prin trei puncte date, puteți merge la ecuația planului în bucăți la ecuația normală a planului, dacă este necesar.

Rămâne să ia în considerare soluția de exemple în care este ecuația planului prin trei mismatched și nu se află pe un punct de linie dreaptă.

Distanța de la punctul de la planul:

Distanța de la punctul de la planul - este lungimea perpendicular dintr-un punct în avion.

Dacă ecuația planul dat Ax + By + Cz + D = 0, distanța de la punctul M (.. Mx My Mz) la planul poate fi găsit folosind următoarea formulă: