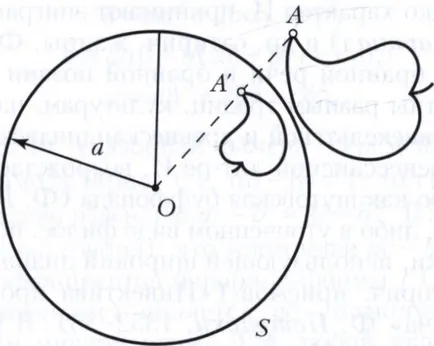
INVERSION în planul de transformare matematică, în care un punct O, care se numește un centru de inversiune, fix și orice punct A, nu coincide cu O, trece la punctul A „situată pe linia OA, astfel încât produsul dintre lungimile segmentelor de linie OA și OA“ este unele număr k, același pentru orice punct A (fig.). Despre centrul de inversiune este numit uneori o inversare pol și k - gradul sau inversarea raportului. Punctele S circumferință cu centrul O și raza √k trece sub inversiune în sine; imagini externe la punctele S sunt puncte de interior, și imagini interne - externe; centru de inversie nu are o imagine. Uneori numit o simetrie inversiune în raport cu cercul. Considerăm, de asemenea, inversiune k<0. Инверсия с отрицательным коэффициентом k равносильна инверсии с тем же центром О и положительным коэффициентом |k|, сопровождаемой симметрией относительно точки О. Инверсия с k> 0 este numit hiperbolic, și cu k <0 - эллиптической инверсией или антиинверсией.
Linia care trece prin centrul de inversie este transformata in sine. O linie dreaptă nu trece prin centrul de inversie este transformat într-un cerc, fără un singur punct. Acest cerc trece prin punctul O și punctul O este exclus din cercul, Reciproca este de asemenea adevărat. Cercul ortogonală la cercul cu centrul O și raza √ | k |, transformate în ei înșiși. În coordonate carteziene, inversiunea centrat la originea poate fi definită prin formulele
sau, în planul complex cu formula z „= k / Z, unde bara denotă conjugare complexă.
inversiune în mod similar cu privire la domeniul de aplicare stabilită în spațiu.
Transformarea Inversiune deoarece 1824 sistematic aplicată matematicianul elvețian J. Steiner.
articole conexe
← genetica Inverse
Inversiune în lingvistică →