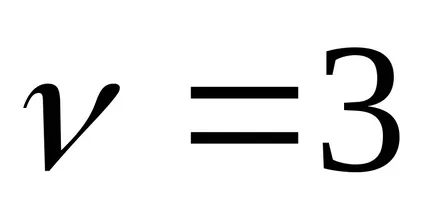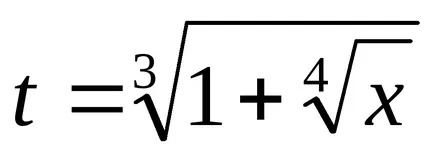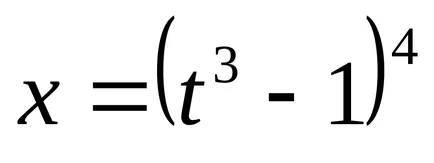Integrarea diferențelor de binomiale

Exemple. Binom numit tip diferențial.

,

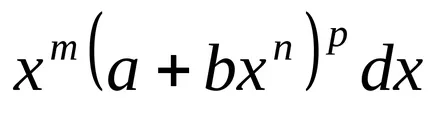
în cazul în care a, b - orice parametri m, n, p - numere raționale. Să ne aflăm cazurile în care aceste expresii sunt integrate într-o formă finită.

Un astfel de caz este direct clar că dacă p - un număr întreg (pozitiv, zero sau negativ), atunci această expresie este de tip studiat în precedent

. Asta este, dacă după denota cel mai mic multiplu comun al numitorilor fracțiunilor și , ceea ce avem aici este o expresie a formei , astfel încât este suficient pentru a raționaliza înlocuirea .

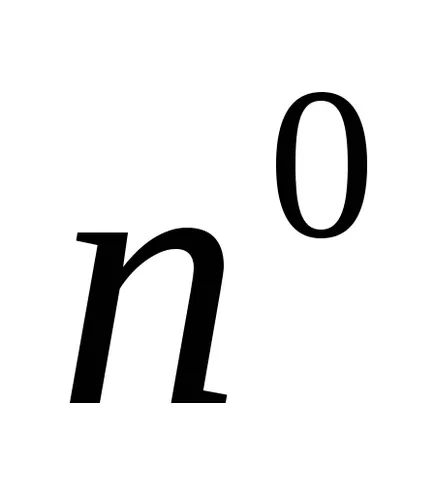
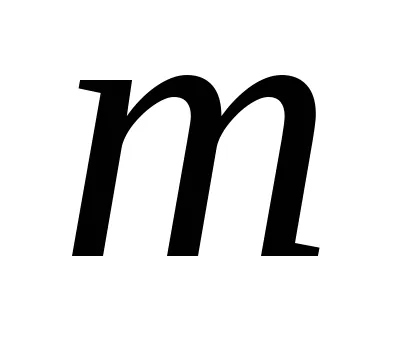
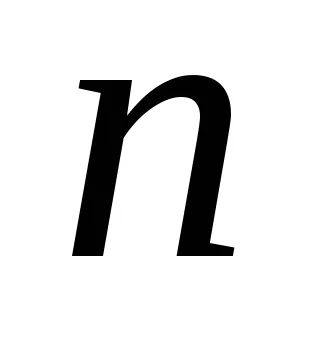
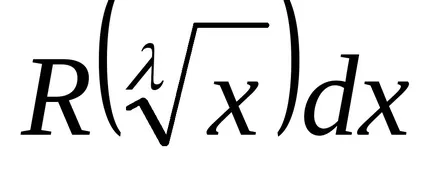
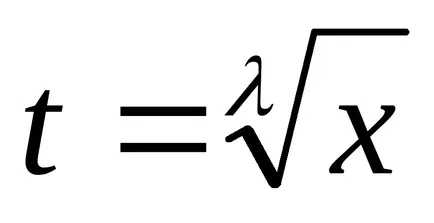
Acum ne transformăm această expresie prin substituirea

.

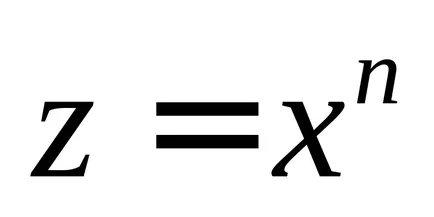
și punerea, de dragul conciziei

,

.

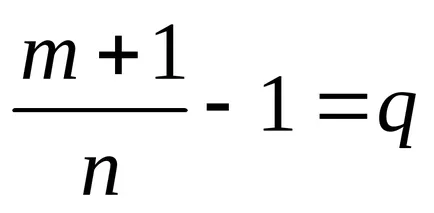
dacă

- un întreg, vom ajunge din nou la expresia tipului studiat. Într-adevăr, dacă vom nota numitorul , expresia convertit este . Raționalizarea integrandul poate fi realizat dintr-o dată - de substituție

.

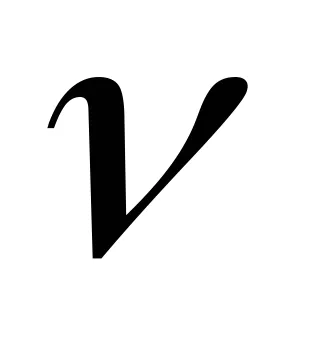
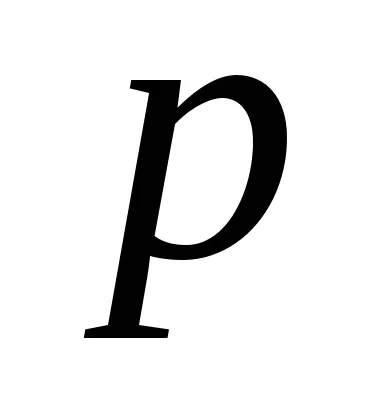
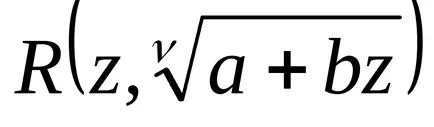
În cele din urmă, a doua rescrierea integrală (2), după cum urmează:

.

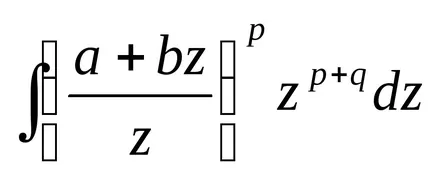
Este ușor de văzut că, pentru

În general, am studiat, de asemenea, cazul: expresia este convertit . Integrandul în această integrală raționalizate și imediat înlocuind

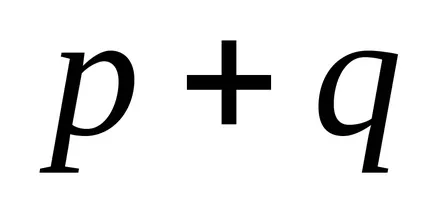
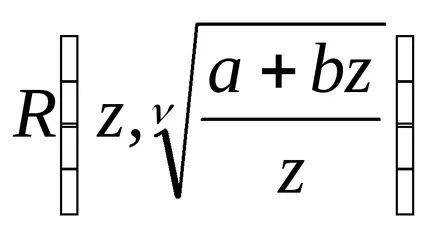
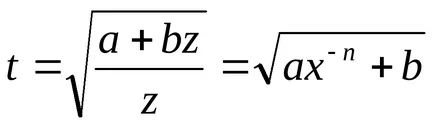
Astfel, atât integral (2) poate fi exprimat într-o formă închisă, dacă întregul este unul dintre numerele

sau (echivalent), unul dintre numerele

.

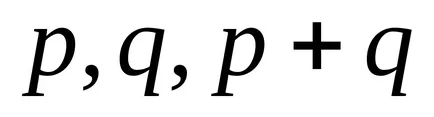
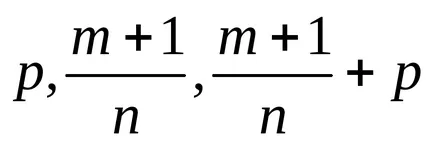
Aceste cazuri integrabile pe fond, erau încă cunoscute de Newton. Cu toate acestea, numai la mijlocul secolului al XlX-lea, PL Cebîșev a stabilit un fapt remarcabil că și alte cazuri de integrabilitate în termeni finite pentru diferentiale binomiali nu.

1). aici

, ,; deoarece

,

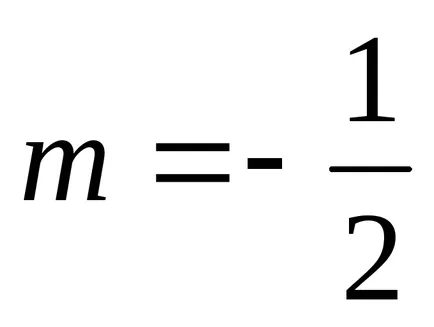
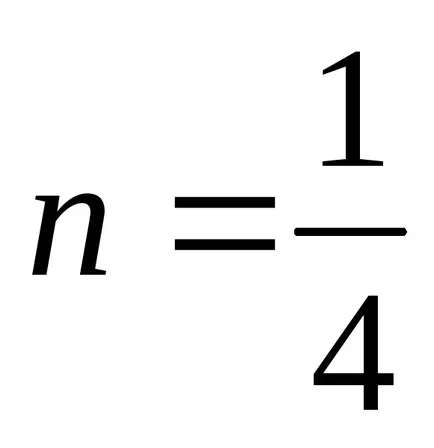
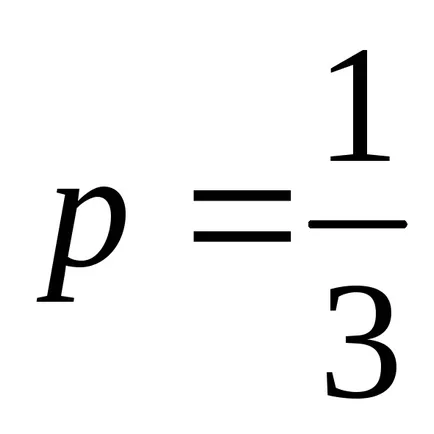
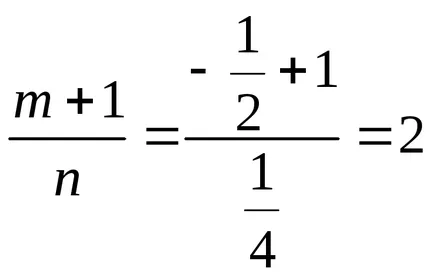
atunci avem de-al doilea caz de integrabilitate. Observând că

, a pus (ca regulă generală)

, , ;