Integrarea Comunicarea cu diferențierea
Luați în considerare integrala definită a cărei limită inferioară este constantă și superioară a schimbat.
Acordarea de limita superioară a diferitelor valori, vom obține valori diferite ale integralei; în consecință, în aceste condiții integralei unei funcții de limita superioară
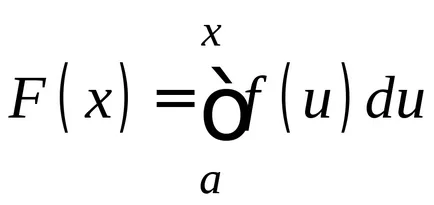
aici

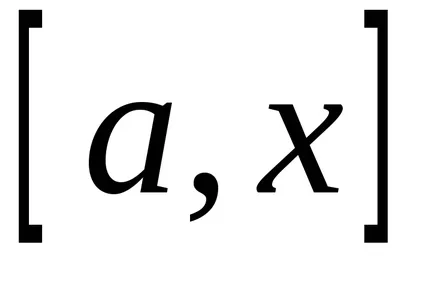
Teorema 1.Proizvodnaya integralei limita superioară este egală cu integrandul
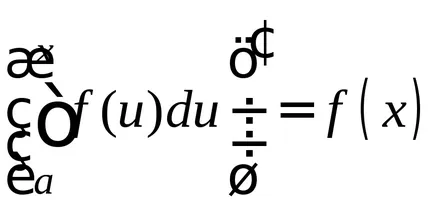
Luați în considerare o valoare a primit nenegativ continuă în intervalul
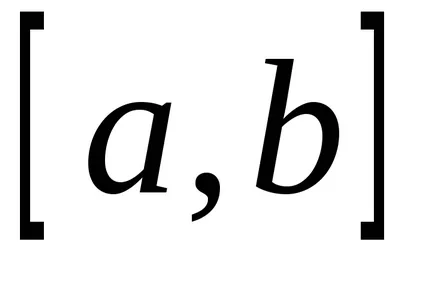
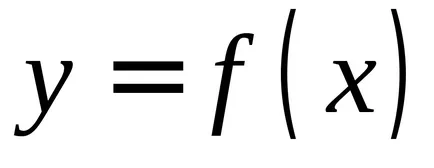

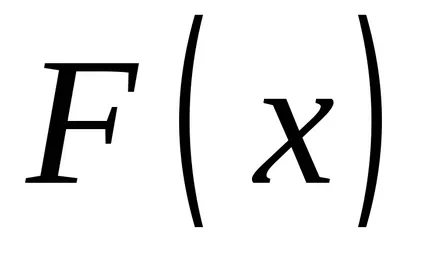
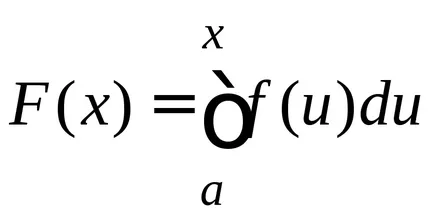
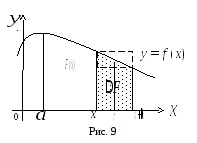
Dacă variabila

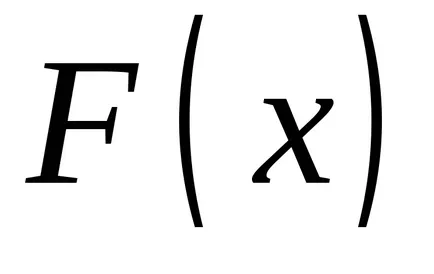

,
unde
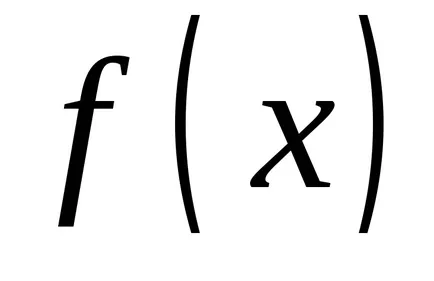
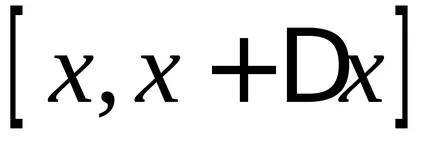


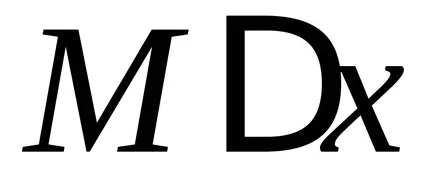

deoarece
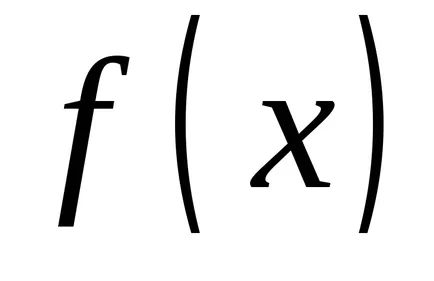
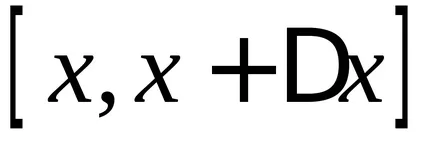
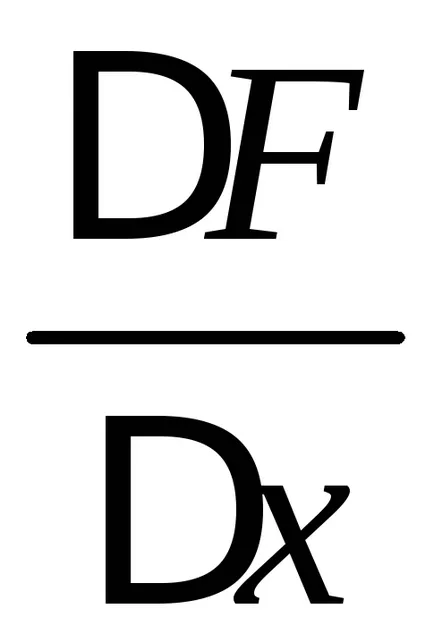
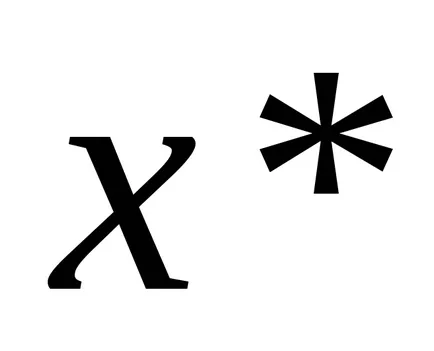
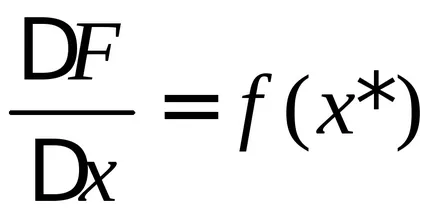
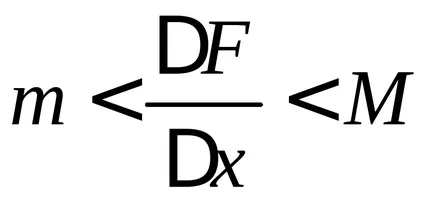
Să considerăm limita acestei expresii cu condiția ca


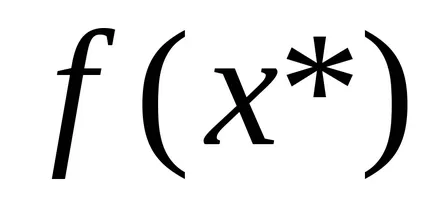
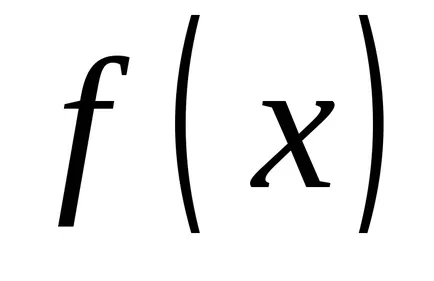
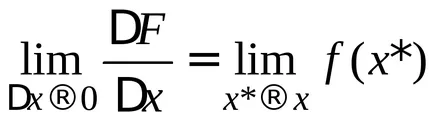
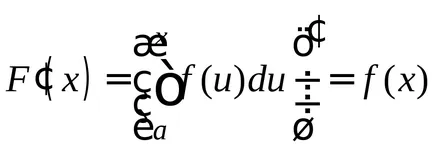
NOTĂ: Această teoremă arată că integrarea și diferențiere - operațiile inverse.
Nedeterminată integrală
OPREDELENIE.FunktsiyuF (x), care este derivata funcției integrantul se numește primitivă.
Cum de a găsi derivat a fost una dintre principalele sarcini ale calculului diferențial, astfel încât găsirea unui primitiv este unul dintre principalele obiective ale calcul integral.
De exemplu, ia în considerare funcția
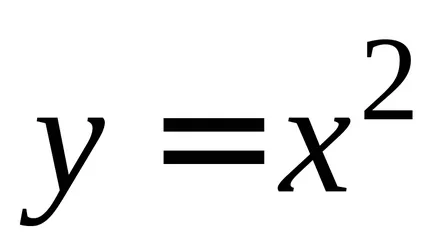
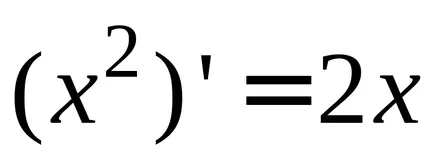
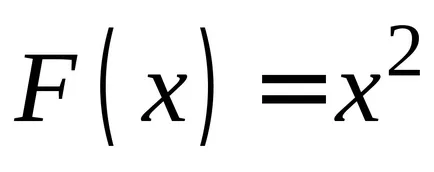
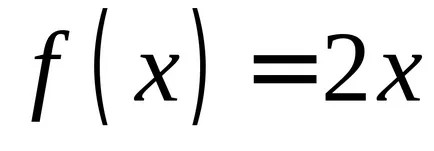
Dacă găsiți derivatele funcțiilor
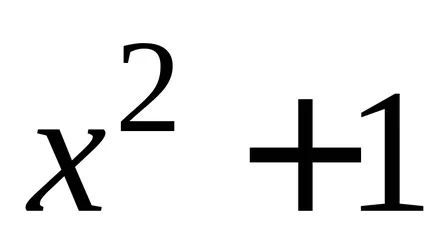
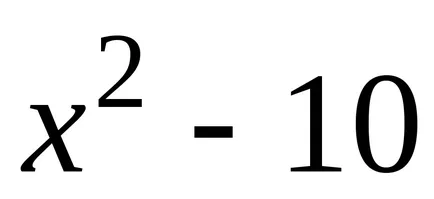
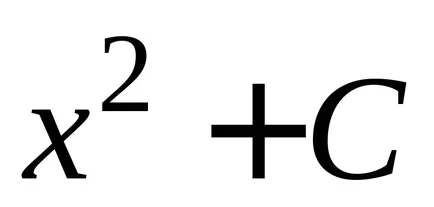

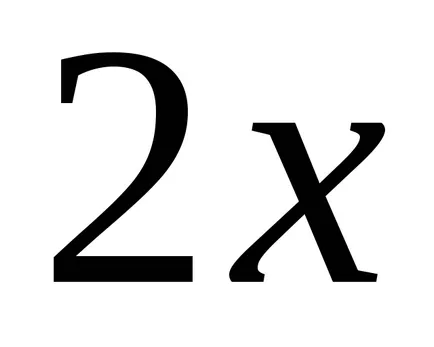
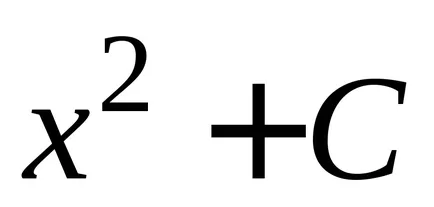
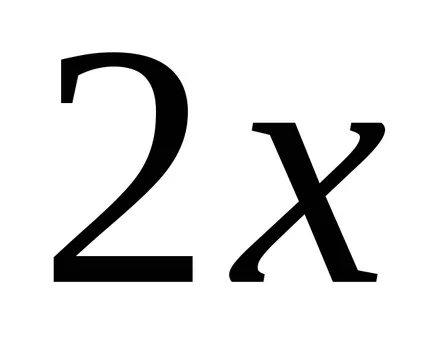
Teorema 2. Orice funcție continuă are un număr infinit de primitive, și oricare două dintre ele diferă unul de altul numai printr-un termen constant.
Să presupunem că funcția
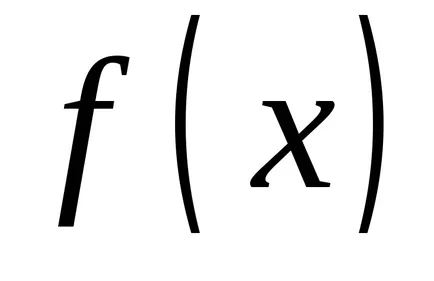
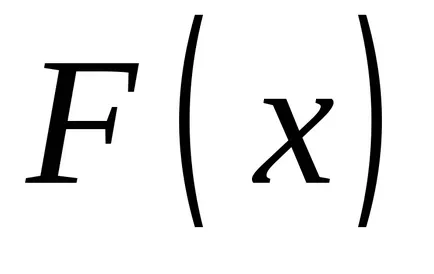
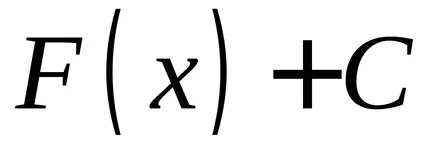

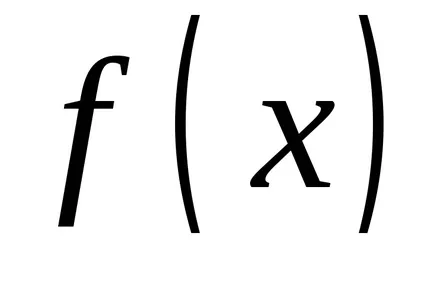
funcţia Să
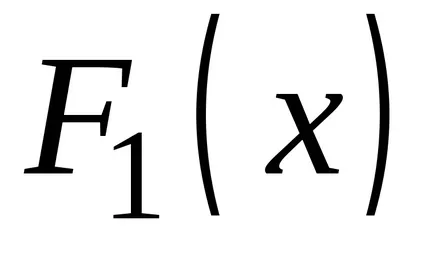
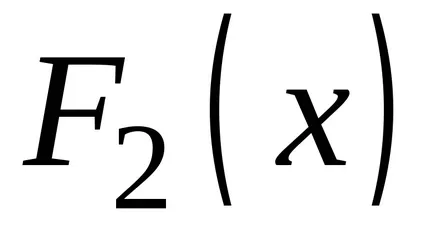
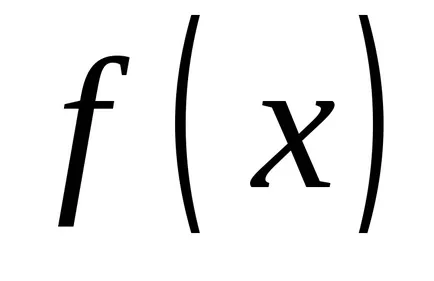
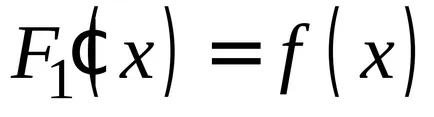
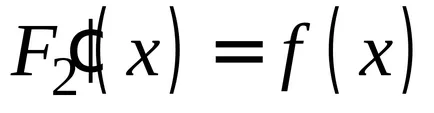
OPREDELENIE.Sovokupnost toate primitivele pentru integrandul se numește integrala nedefinită.
Integrala nedefinită este, de asemenea, menționată ca fiind specifică, numai fără frontiere, și anume dacă
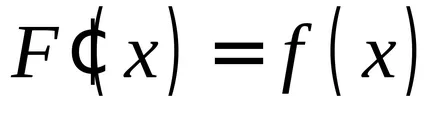
.
și

,
,
.
Funcția primitivă Program
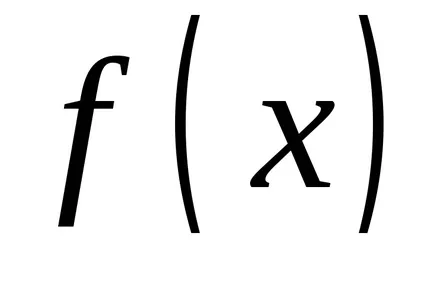
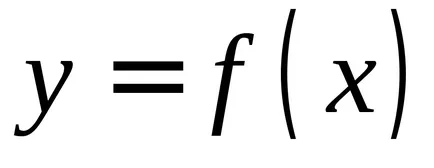
Din definiția integralei nedefinită ca o pluralitate de primitivelor
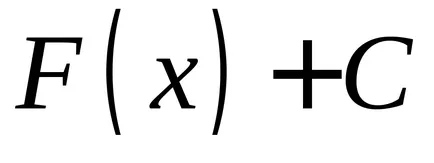
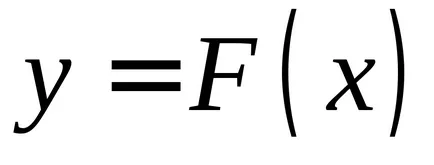

Tabelul 1 prezintă derivații și primitivele de bază pentru funcțiile elementare.