incircle
unde p - jumătate de perimetru al triunghiului, h o. h b. h c, h_> - înălțimea realizată pe laturile respective ale [1];
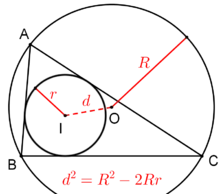
- Dacă A B - baza unui triunghi isoscel △ A B C. tangenta cercului pe laturile unghiului ∠ A C B la punctele A și B. Se trece prin centrul cercului inscris triunghiului △ A B C.
- Teorema lui Euler. R 2 - 2 R r = | O I | 2 -2Rr = | OI | ^>. unde R - raza unui triunghi în jurul circumferinței, r - raza unui cerc înscris în ea, O - circumscris, I - centrul cercului inscris.
- În cazul în care linia dreaptă care trece prin punctul I paralel cu latura AB, BC și CA intersectează laturile de la punctele A1 și B1. atunci A 1 B 1 = A 1 + A B B 1 B_ = a_b + AB_>.
- Punctul de triunghi tangență T înscris într-un cerc conectat segmente - se obține triunghi T1
- bisector T sunt midperpendiculars T1
- Să T2 - T1 ortotreugolnik. Apoi mâna lui paralelă cu laturile T. triunghi original,
- Să T3 - mijlocul triunghiului T1. În timp ce bisectoare T sunt înălțimile T3.
- Să T4 - T3 ortotreugolnik. în timp ce T bisectoare sunt Bisectors T4.
- Raza înscris într-un triunghi dreptunghic cu picioare a, b și c ipotenuza este egal cu circumferința a + b - c 2 >>.
- C Distanța de la vârful triunghiului până la punctul în care cercul inscris atinge laturile, este egală cu d = a + b - c 2 = p - c> = p-c>.
- Distanța de la vârful la centrul C al cercului inscris este egal cu l c = r păcat (γ 2) =>) >>>. unde r - raza cercului înscris, și γ - unghiul la vârf C.
- Distanța de la vârful la centrul C al cercului inscris pot fi găsite prin formulele l c = (p - c) 2 + r 2 = + r ^ >>> și l c = a b - 4 R r = >>
- Teorema pe tridentul sau teorema trifoiul. Dacă D - punct de trecere a bisectoarea unghiului A cu cercul circumscris triunghiului ABC. I și J - centre respectiv inscriptionare cerc tangente este descris de partea BC. atunci | D I | = | D B | = | D C | = | D J | .
- Lema Verrier [2]. Fie V cerc tangente la laturile A B. A C și B C din circumferința arcului triunghiului A B C. Apoi, punctele de tangență a cercului V cu laturile și centrul cercului inscris triunghiului A B C minciuna pe o singură linie.
- Teorema lui Feuerbach. În ceea ce privește noua puncte cerc toate cele trei cercuri este descris. și cercul inscris. Punctul tactil Euler cerc și cercul înscris este cunoscut sub numele de punctul Feuerbach.
Comunicarea cu cercul circumscriere cercului inscris
unde p - triunghi semiperimetrul, S - zona sa.
- Perpendicularele vosstavlennye pe laturile triunghiului în punctele de tangență ale cercurilor se intersectează la un este descris punct. Acest punct central simetric al cercului inscris în jurul centrului cercului [4].
- Pentru un triunghi se poate construi cerc poluvpisannuyu sau cerc Varera. Acest cerc tangent la două laturi ale unui triunghi și cercul circumscris intern. Segmentele care leagă nodurile respective ale unui triunghi și punctele de tangență cu cercul circumscris Verrier. se intersectează la un moment dat. Acest punct este centrul de dilatare cu un coeficient pozitiv, care ia în cerc înscris descris.
- Centrul cercului inscris se află pe segmentul care leagă punctele de laturile de contact ale triunghiului și cercul poluvpisannoy.
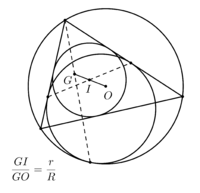
Poluvpisannaya circumferința și centrul homothety G pentru cercuri și circumscrise inscripționate cu raze r și R, respectiv,
- patrulater descrise. dacă el nu are nici o auto-intersectii ( „simplu“), trebuie să fie convexă.
- Unele (dar nu toate) din patrulaterele au un cerc înscris. Ele sunt numite patrulater circumscris. cel mai important este faptul că suma de laturi opuse sunt printre proprietățile acestor patrulatere. Această afirmație se numește o teoremă a Pitot.
- Cu alte cuvinte, ABCD patrulater convex în cerc poate fi înscris dacă și numai dacă suma dintre laturile sale opuse, egal cu: A + B C D = B C + A D.
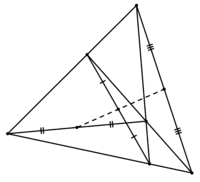
- Cel puțin două mijlocul descrise patrulater diagonalele și centrul cercului înscris sunt coliniare (teorema lui Newton). Este, de asemenea, segmentul de mijloc, cu puncte finale de intersecție dintre extensiile laturile opuse ale unui patrulater (în cazul în care nu sunt paralele). Această linie se numește linie Gauss. Cifra este verde, roșu diagonală, se taie capetele la punctele de intersecție ale extensii de laturile opuse ale unui patrulater este, de asemenea, de culoare roșie.
- Centrul descris despre circumferința patrulaterului - înălțimi ale punctului de intersecție al triunghiului cu noduri la punctul de intersecție al diagonalelor și punctele de intersecție ale laturilor opuse (Brocard teorema).
În triunghiul sferic
Cercul înscris al triunghiului sferic - o tangentă cerc la toate laturile sale.
- Tangenta raza [5] al cercului înscris în triunghiul sferic este egal cu [6]: 73-74
- Înscrisă în cercul triunghi sferic aparține sferei. Raza trase din centrul sferei prin centrul cercului inscris intersectează sfera în punctul de intersecție al Bisectoarele unghiurilor (arce ale marilor cercuri ale sferei, împărțind unghiul în jumătate) triunghi sferic [6]: 20-21.
O serie de note scurte care nu sunt conținute în articol, sau nu conduce la secțiunea „Referințe“.