încărcare Edelennaya

În cazul în care decizia nu este întotdeauna probleme practice, se poate presupune că acționează asupra corpului forța este aplicată la un moment dat. Forțele sunt adesea aplicate pe întreaga suprafață a corpului (de exemplu încărcătura de zăpadă, vânt etc.). Aceasta se numește o sarcină distribuită. Caracterizat printr-o q intensitate sarcină distribuită uniform (Figura 1.29). Intensitate - este sarcina totală pe unitatea de lungime a structurii.

Unitatea de măsurători de intensitate [H / m], [kN / m]. Când rezolvarea problemelor staticii distribuite de încărcare poate fi înlocuită cu rezultanta care este egală cu produsul intensității pe lungimea porțiunii care acționează asupra sarcina distribuită, și care este atașat la mijlocul acestei porțiuni.

1.13. Solutia problemelor pe un sistem de forțe plat

Exemplu (Figura 1.30). Se determină forța fasciculului încărcate reacție simplu rezemate

și o pereche de forțe cu momentul M.

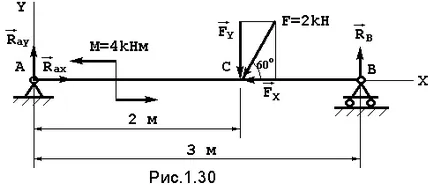
Decizie. Noi folosim același plan, care a fost utilizat pentru rezolvarea problemelor în forțele convergente ale sistemului. Obiectivul este de a echilibra întregul fascicul, sarcina care este prezentată în desen. Picătură conexiunea - balamalelor A și B. Reacția balamalei fix descompus în două componente -

și, și reacția în articulația mobilă este îndreptată perpendicular pe planul de referință. Astfel, grinda acționează sistem arbitrar plat al forțelor la care este posibil să se facă trei ecuații de echilibru. Selectați o axă de coordonate și compun aceste ecuații. Ecuațiile proeminentelor:

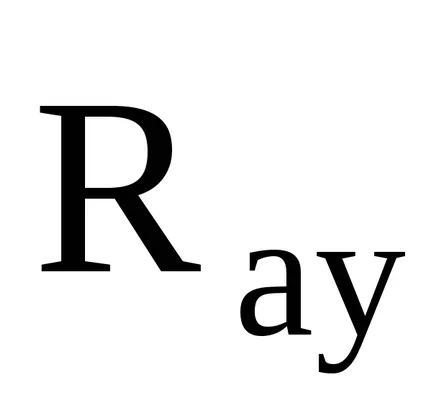
(O pereche de proeminențe în ecuație nu este inclus, deoarece suma proiecțiilor perechii de forțe pe orice axă este zero).

momentul Ecuația este relativ la punctul A, deoarece este traversat de două forțe necunoscute. Dacă găsiți timp în ceea ce privește o pereche de puncte A amintesc că suma momentelor de forțe cu privire la orice pereche de puncte este egal cu timpul perechii, iar în momentul în care semnul este pozitiv, deoarece perechea tinde să se rotească în sensul acelor de ceasornic corpul. Pentru a găsi momentul forței

este convenabil să se extindă componentele verticale și orizontale:

și de a folosi teorema lui Varignon, și trebuie remarcat faptul că în momentul de forță

în raport cu punctul A este egal cu zero, deoarece linia de acțiune trece prin acest punct. Apoi ecuația momentelor ia forma:

3.

; RB. 3-FB cos (30) 2 + M = 0.

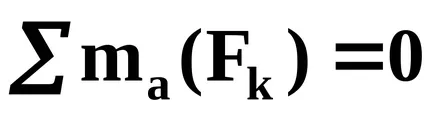
Rezolvarea acestei ecuații obținem:

Din ecuația (2) găsim: