Hraneste vector câmp electric

flux Vector $ \ overrightarrow \ $ suprafață prin $ S numit $ valoare algebrică $ _a $, care este definit după cum urmează:

Semnul fluxului depinde de alegerea direcția normală la zona elementară $ dS $.

vector intensitate flux elementar

Referindu-se la câmpul electric. Intensitatea modulului este egal cu numărul de linii de câmp care se intersectează suprafața, care este egală cu una, suprafața trebuie să fie perpendicular pe liniile câmpului în locul dat. Numărul de linii de câmp care traversează suprafața numit mai sus, numit vectorul flux de tensiune. Dacă suprafața evidențiați zona elementară (dS), pentru a construi un normal la acest site $ \ overrightarrow $, în care unghiul dintre vectorul normal și vectorul de direcție din suma $ \ alpha $, fluxul elementar al vectorului intensitate ($ $ dF_E) poate fi scrisă ca:

\ [DF_E = EdScos \ alpha = \ overrightarrow \ cdot d \ overrightarrow \ \ stânga (2 \ dreapta) \]

În ecuația (3) $ \ overrightarrow unitate $ normală pentru site-ul $ dS $.

Dacă luăm în considerare orice - sau orice suprafață $ S $, putem scrie că intensitatea fluxului vectorului ($ $ F_E), în conformitate cu definiția vectorului (1) Debit:

\ [F_E = \ int \ limits_S \ cdot d \ overrightarrow> \ \ \ din stânga (4 \ dreapta). \]

Sensul normal

Ca și în cazul general, vectorul de curgere al valorii algebrice. semn de curgere depinde de configurația terenului și direcția vectorului - normal $ \ overrightarrow $. Direcția condiționat normală. Se poate spune că integrala din ecuația (4) reprezintă vectorul sursă de putere $ \ $ overrightarrow totală, cu care sunt taxele în interiorul volumului, care limitează suprafața $ S $.

Se consideră că, atunci când se ocupă cu o suprafață închisă, direcția normală este pozitiv afară. Curgerea vectorului intensitate în cazul unei suprafețe închise este înregistrată printr-o linie integrală de-a lungul unei suprafețe închise:

\ [F_E = \ oint \ limits_S \ cdot d \ overrightarrow> \ \ \ din stânga (5 \ dreapta). \]

Target: intensitatea câmpului electric este dat de formula în coordonate carteziene:

unde $ \ overrightarrow, \ \ $ overrightarrow - vectori unitare ale OX și OY axelor. Găsiți fluxul vectorului $ \ $ overrightarrow printr-o suprafață sferică, în cazul în care raza sa este egală cu R $ $, iar centrul său se află la originea.

Ca bază pentru soluția folosind definiția vectorului flux de tensiune, și anume:

\ [F_E = \ int \ limits_S \ cdot d \ overrightarrow> \ \ \ din stânga (1,1 \ dreapta), \ \]

în cazul în care $ d \ overrightarrow = \ overrightarrowdS $, $ $ DS- elementare de suprafață sferă spațiu, $ \ overrightarrow $ - normal pentru acest domeniu.

Scriem expresia normala la suprafața sferei, sub formă de:

Înlocuim (1.2) în (1.1), folosind expresia intensității câmpului condițiilor problemei, vom găsi integral, astfel, atunci când produsul în integrandul, consideră că $ \ overrightarrow, \ overrightarrow, \ overrightarrow $ - vectori unitate ortogonale.

Ținta: Determinarea vectorului de curgere prin tensiunea de suprafață sferică, în cazul în care se află cele două taxe punctul de $ + q_1 $ și $ $ _2.

Ca bază pentru decizia poate lua pentru formula de flux de intensitate vector ca:

\ [F_E = \ overrightarrow \ cdot S \ overrightarrow = ESCOs \ alpha \ \ stânga (2.1 \ dreapta) \]

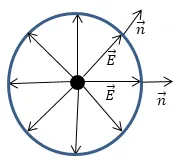
unde $ \ alpha $ - unghiul dintre normala la suprafață prin care se caută și fluxul vectorului intensitate. câmp de încărcare punct are simetrie sferică (figura 1). Prin urmare, vectorul și intensitatea câmpului vectorial - normale sunt codirectional ($ cos \ alpha == $ 1). Fig. 1 prezintă un câmp de o sarcină pozitivă.

Intensitatea câmpului rezultat poate fi obținut în conformitate cu principiul superpoziției câmpurilor celor două taxe, cu caractere.

Scriem expresia pentru câmpul modul, care creează o primă taxă:

Pentru a doua taxa:

Am găsit modulul tensiunilor rezultate, având în vedere faptul că sarcina pozitivă - sursa câmpului, iar negativ - câmpul de curgere, adică, direcția opusă domeniile:

Dacă ne uităm pentru curgerea prin sfera care are o rază R, atunci expresia (2.4) ia forma:

Suprafața unei sfere (S) este egală cu o rază predeterminată:

În acest caz, înlocuiți expresiile (2.6) și (2.5) până la (2.1), observăm că $ cos \ alpha == $ 1, obținem: