funcție liniară și graficul acesteia, matematici superioare - simple și ușor
În ultima lecție ne-am uitat la proporționalitate directă și graficul acesteia. Vom lua în considerare acum o funcție mai complexă, ci ca un complex doar un pic mai complicat.
Luați în considerare exemplele de funcții
Exemplul 1. Distanța dintre cele două orașe (A notat și B) este de 30 km. Motociclist stânga punctului B, în direcția opusă A, la o viteză de 50 km / h. Timp de câteva ore călăreț va trece de kilometri și va fi orașul A, la o distanță de kilometri. Dacă notăm distanța de la litera A la călăreț orașului, dependența distanței de timp poate fi exprimată prin formula
,
EXEMPLUL 2 elev a cumpărat notebook-5 ruble bucata și cu mânerul 10 de ruble. Notăm numărul de notebook-uri achiziționate cu litera, iar costul tuturor achizițiilor. Atunci vom obține
,
unde x - întreg.
definiție
În acest exemplu, ne-am întâlnit cu funcțiile care sunt definite prin formulele
,
în cazul în care - o variabilă independentă, și și - numărul.
Aceste funcții sunt numite funcții liniare.
funcție liniară este o funcție care poate fi definită prin formula formei în care - variabila independentă, și și - unele numere.
directă proporționalitate, pe care am studiat în ultima lecție, de asemenea, se referă la o funcție liniară, dar acesta este un caz special, în cazul în care al doilea număr nu este prezent sau este zero.
Acum, să aflăm ce programul este o funcție liniară.
Ca un exemplu, să ia funcția simplă, care corespunde formulei, și se compară cu o valoare direct proporțională cu aceleași valori.
Deja pornind de la valorile ambelor funcții poate observa că pentru orice valoare a valorii x argument funcție de 4 unități mai mici decât funcția de valoare
Acum vom construi grafice
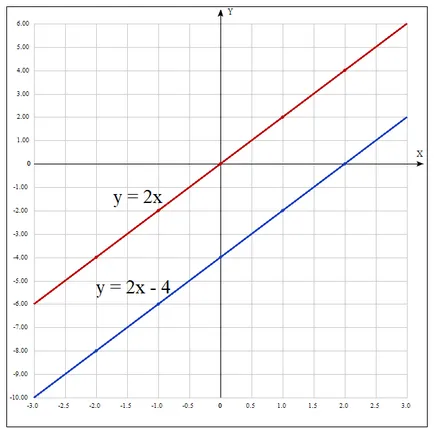
După cum puteți vedea pe grafic, liniile de date sunt paralele.
Graficul functiei, unde k ≠ 0, există o linie dreaptă paralelă cu linia.
De altfel, există cazuri în care k = 0, ecuația ia forma în care graficul funcției va fi paralelă cu axa X, și având o valoare egală cu argumentul cu numărul b.
De exemplu, vom construi un grafic al unei funcții y = 2
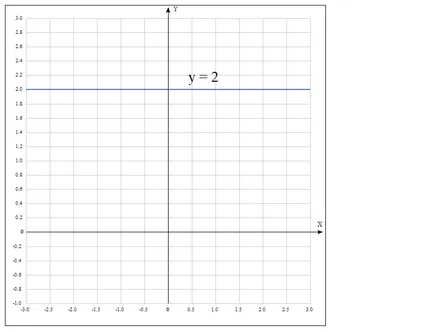
Această funcție este, de asemenea, liniară.
Pentru a construi linia de doar două puncte, după cum direct proporțională cu un punct a fost cunoscut, am găsit doar un singur punct, în aceeași funcție liniară, avem nevoie pentru a găsi cele 2 puncte.
Ei bine, asta e tot, cum ți-am spus totul, astfel încât să puteți termina.