Funcția y TGX, ctgx y, proprietățile și graficele lor

§ 15. Funcții y = tgx, y = ctgx, proprietățile și programele lor

Notă proprietățile funcției y = tg x, și în special a celor care contribuie la a face o reprezentare despre graficul (majoritatea acestor proprietăți sunt de fapt cunoscute la noi de la § 5). Atunci când o astfel de prezentare merge bine, vom începe să construim un program, ca de obicei, pe puncte.

Proprietatea 1. Domeniul funcției y = tg x - set de numere reale, cu excepția numerelor de forma

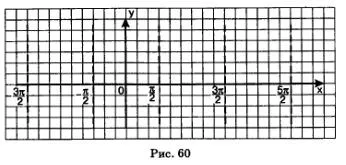
Această proprietate înseamnă că funcția graficului nu este punctul, nu este deținut de punctul directă care aparține unei linii drepte nici un punct aparținând unei linii drepte, etc. Aceste linii deținute de linii punctate în Fig. 60.

Prima prezentare a graficului obținut prin: ea constă dintr-un număr infinit de ramuri (în banda
Proprietatea 2. y = tg x funcție periodică cu o perioadă de n fundamentală.
Acest lucru rezultă din ecuația obținută în dublu § 5.
Deci, dacă vom construi o sucursală grafic în banda de atunci va trebui să se mute ramura construit de-a lungul axei x la dreapta și la stânga de n, 2n, Sn, etc. Teck obține astfel o a doua imagine a graficului.

3. Proprietatea in = tg x este o funcție ciudată. Rezultă din ceea ce a fost demonstrat în raport § 5 program funcția de ciudat simetrică cu privire la originea. Deci, putem proceda după cum urmează: să se bazeze pe o parte a punctelor de teren pe intervalul de la și apoi să profite de această simetrie.

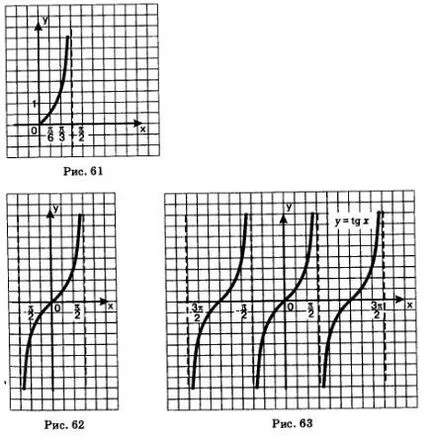
Să ne construim grafic pe intervalul. Selectați un punct de control:

Notă aceste puncte pe un plan de coordonate și trage o curbă lină prin intermediul lor (Fig. 61). Adăugați curba linie construită simetric în raport cu originea (Fig. 62). Folosind intervale completează graficul până la capăt (fig. 63).

Graficul y = tg x tangensoidoy numit. Acea parte care este prezentat în Fig. 62, denumit în mod obișnuit ca principal tangensoidy ramură.

Rețineți că originea tangensoidy ramura principală ca în cazul în care, la un unghi de 45 °. De ce acest lucru este așa, veți învăța în Capitolul 4.

Proprietatea 4. Funcția mărește intervalul într-un mod mai general - funcția este în creștere pe orice interval de forma
Proprietatea 5. Funcția y = tg henna limitată, fie de sus sau de jos.

6. Funcția de proprietate în x = tg nici cea mai mare sau cea mai mică valoare Sheha.
Proprietatea 7. Funcția y = tg x este continuă pe intervalul într-un mod mai general - este continua pe orice interval de forma
În cazul în care valoarea funcției este discontinuă. Fiecare linie este un fel de grafic asimptotoi verticală a funcției.

Deci, și acest lucru înseamnă o creștere a funcției y = tg x pe intervalul selectat.
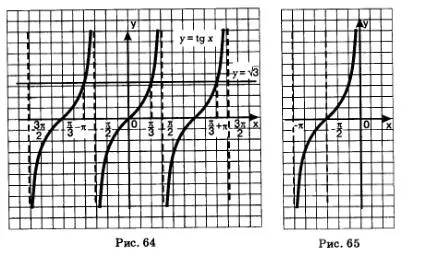
Exemplul 1. Rezolva ecuatia x = tg
Decizie. Construit în una grafică sistem de funcții de coordonate y = tg x - și y = tangensoidu - linia paralelă cu axa x. Ei au infinit mai multe puncte de intersecție (Fig. 64), iar abscisele punctelor diferă unul de altul pe PC. La principalele ramuri ale abscisa punctului corespunzător este (am folosit cunoscut egalitatea numerică - este una rădăcină a ecuației și toate soluțiile sunt descrise prin formula
răspundă:

Exemplul 2. Funcția Plot
Decizie. Pentru a începe, să se ocupe cu principalul tangensoidy ramură.
1) procedează la auxiliar sistemul de coordonate cu originea în punctul a avut loc la Fig. ) 65 linia punctată.
2) Funcția "Tie" in tg = x * nou sistem de coordonate - aceasta este funcția program. mai degrabă, ramura principală a graficului dorit (vezi Figura 65 -. curba solidă).
3) Pentru a obține graficul funcției afișare suficient construit ramură simetric în raport cu axa x (fig. 66).
4) Cunoscând o ramură, puteți construi un întreg grafic (fig. 67).

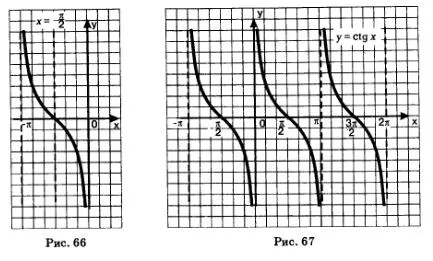
De fapt, în Fig. 67 construit de graficul y = stgh. De ce? Deoarece identitatea (formula de reducere)
Graficul funcției y = x CTG ca graficul funcției y = tg x, numit tangensoidoy. Ramura principală a graficului funcției y = x CTG numit de obicei ramură închisă în banda de la x = 0 până la x = k.
Exemplul 3: rezolva ecuația CTG x = -1.

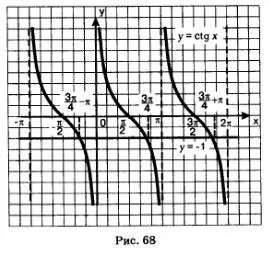
Decizie. Construim într-un sistem de coordonate funcții grafice y = x CTG - tangensoidu și y = -1 - o linie paralelă cu axa x. Ei au un număr infinit de puncte de intersecție (fig. 68), iar abscisă acestor puncte sunt diferite unele de altele în Jap. La principalele ramuri ale abscisa corespunzătoare punctului este (am folosit relația bine-cunoscut: și toate soluțiile ecuației dat pot fi acoperite de formula
răspundă:

AG Mordkovich Algebra Grad 10

Dacă aveți corecturi sau sugestii la această lecție, vă rugăm să ne contactați.

Dacă doriți să vedeți alte ajustări și sugestii pentru lecții, uita-te aici - Forumul Educațional.