Funcția Y kx și graficul acesteia

Graful «y = kx» este dreaptă.

Amintiți-vă de la axioma geometrie (o declarație care nu are nevoie de o dovadă) că două puncte, poți desena una dreaptă și numai unul.

Pe baza acestei axiome care a realiza un grafic funcțiile de forma „y = kx» va fi suficient pentru a găsi doar două puncte.

De exemplu, vom construi un grafic «y = -4x» funcția.

Găsim valoarea funcției «y» pentru două «x» valori arbitrare. Substitut, de exemplu, în loc de «x» numere „0“ și „1“.

Alegerea valori numerice arbitrare în loc de „x“, mai bine să ia numărul „0“ și „1“. Cu aceste numere ușor de a efectua calcule.

y (0) = -4 · 0 = 0

y (1) = -4 · 1 = -4

Valorile obținute din «x» și «y» - coordonatele punctelor graficului
Funcția «y = -4x».

Înregistrați coordonatele punctelor «y = -4x» în tabel.

Notă punctele de date privind sistemul de coordonate.

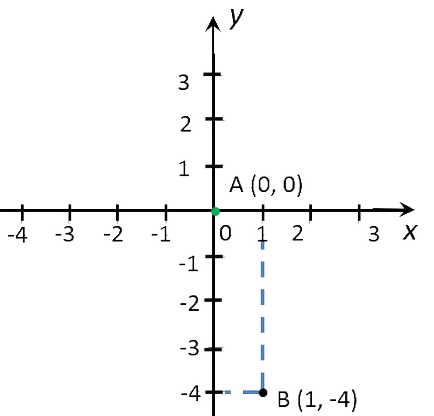
Acum, trage o linie dreaptă prin punctele reprezentate grafic. Această linie va fi graficul funcției «y = -4x».

După construirea nu uitați să semneze graficul funcției.

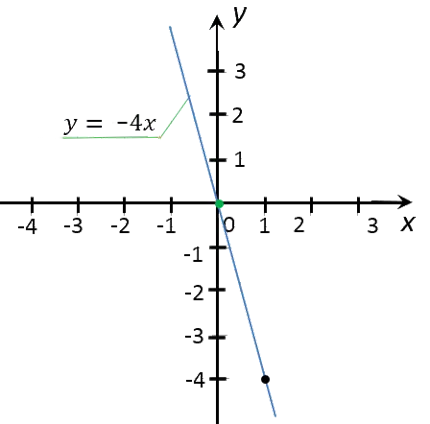
Cum de a rezolva problema pe funcția «y = kx»

Se trasează «y = -1,5x» funcția. Găsiți programul:

1. Valoarea «y» corespunzătoare valorii «x» este egal cu 1; 0; 2; 3;
2. Valoarea «x», în cazul în care valoarea «y» este egal cu -3; 4.5; 6;
3. unele întreg «x» valoarea la care valoarea «y» pozitiv (negativ).

Noi construim mai întâi un grafic al funcției «y = -1,5x».

Noi folosim regulile prin care noi reprezentate grafic funcțiile de mai sus. Pentru a construi graficul funcției «y = -1,5x» suficient pentru a găsi doar două puncte.

două valori numerice arbitrare am ales pentru «x». Pentru comoditatea calculelor vom alege numărul de „0“ și „1“.

Vom efectua calcule și scrie rezultatele în tabel.

Coordonată pe axa „Ox“

Notă punctele de date de pe un sistem de coordonate rectangulare.

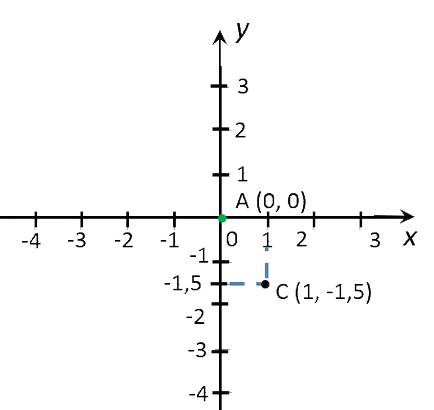
Conectarea a primit un punct direct. Organizarea de directe va fi programul «y = -1,5x» funcția.

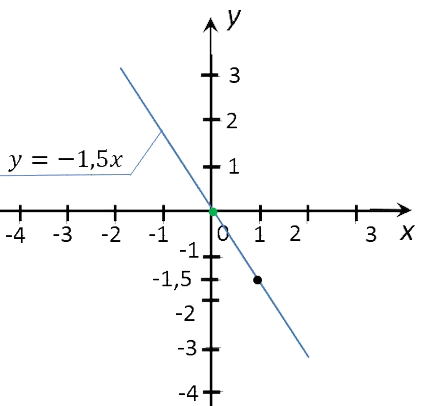
Acum lucrăm cu diagrame funcții «y = -1,5x».

Necesar pentru a găsi valoarea «y», care corespunde valorii «x» este egal cu 1; 0; 2; 3.

„Cum să obțineți coordonatele punctelor funcției“, cu graficul funcției am analizat deja în detaliu în tutorial „Cum de a rezolva problema într-o funcție.“

În această lecție pentru a rezolva problema de mai sus amintiți-vă doar scoate în evidență.

Pentru a găsi valoarea «y» cunoscută valoare «x» în funcția de graficul necesar:

1. perpendiculara de la «Ox» axa (abscisa) unei valori numerice predeterminată «x» până la intersecția cu graficul funcției;
2. obținută din punctul de intersecție al funcțiilor grafice perpendicularei și să dețină un alt perpendicular pe «Oy» axa (ordonată);
3. valoare numerică obținută pentru «Oy» axă este valoarea dorită.

În conformitate cu regulile de mai sus, vom găsi pentru «y = -1,5x» «y» funcțiile necesare valori de diagramă construite anterior pentru «x» este 1; 0; 2; 3.

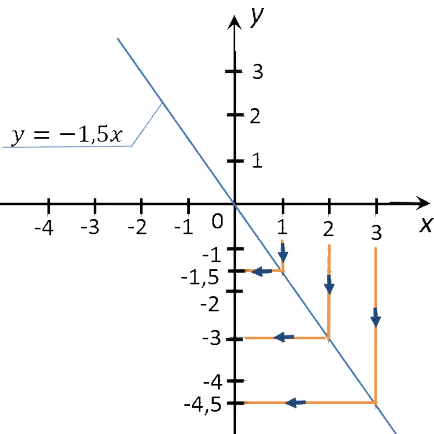
Înregistrați rezultatele în tabel.

Valoarea prestabilită «x»

A primit din grafic valoarea «y»

Și, în sfârșit, ultima sarcină. Am cerut să găsim mai multe numere întregi «x» valoarea la care valoarea «y» pozitiv (negativ).

Pentru a rezolva această problemă este necesar să se studieze cu atenție
graph «y = -1,5x» funcția.

Notă Zona pe «Oy» axa, unde valorile «y» pentru graficul «y = -1,5x» pozitiv.

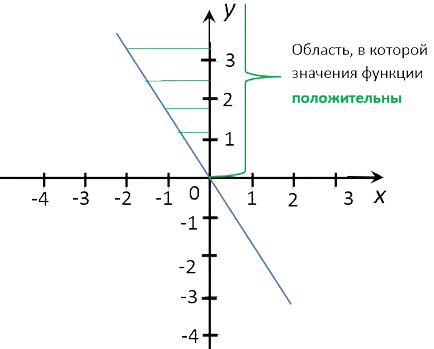
Din această zonă cheltui pe grafică are mai multe perpendiculare «Ox» axe.

Amintiți-vă că pe instrucțiunile, ni se cere să găsească unele „» «x» valori întregi. Prin urmare, vom efectua perpendicularele la «Ox» axa în valorile numerice întregi.

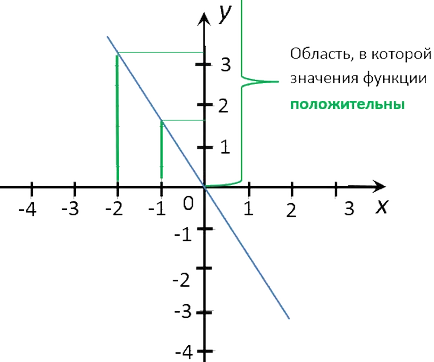
Scriem răspunsul. Când x = -2; x = -1 valori y> 0.

Acum vom găsi în orice «x», valorile «y» negativ. Notă Zona pe «Oy» axa, unde valorile «y» în funcția negativă graficului.

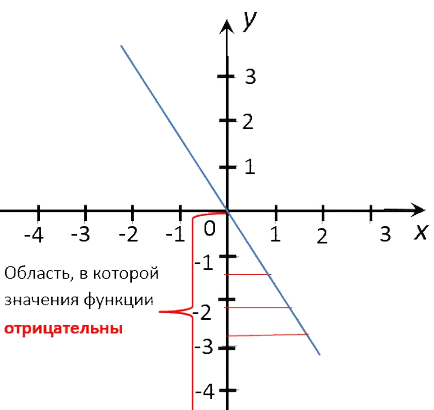
Egal perpendicularele din zona marcata a «Ox» axe întregi valori numerice «x».

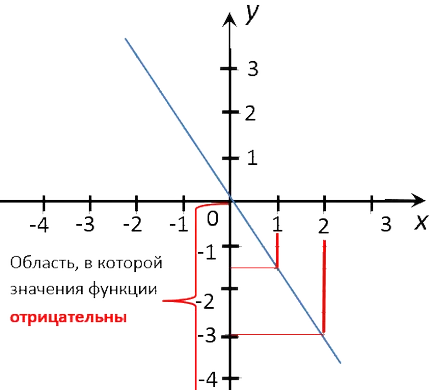
Scriem răspunsul. Când x = 1; x = 2, valorile y

Luați în considerare o altă sarcină.

Care dintre punctele A (5, 3). D (2, 1) aparțin funcției grafică dată
formula «y =