Funcția de distribuție selectivă
Pentru variabila aleatoare empirică, având în vedere legea empirică de distribuție, este posibil să se înregistreze și de a construi o funcție de distribuție personalizată.
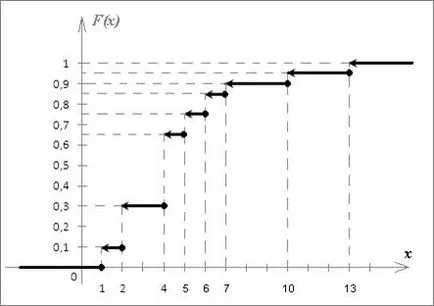
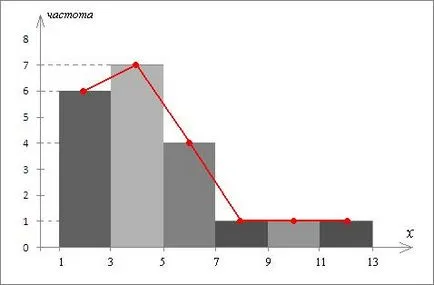
funcție variabilă aleatoare definită pe axa întregii reală și definită de ecuația: F (x) = P (# 958; Când x ≤ 1 eveniment # 958; 20 <1 невозможно, т.к. нет значений ξ20 меньше 1, а вероятность невозможного события равна нулю, следовательно, În intervalul 1 In intervalul 2 În intervalul 4 Diferența de 5 Astfel, funcția de distribuție selectivă este: Se determină valoarea funcției de distribuție pe axa întregii reală, este posibil să se construiască graficul ei (figura 1). Funcția Program de distribuție selectivă are o formă în trepte și este construit în formă de segmente: valoarea cea mai mică din stânga (x = 1), valoarea funcției este 0 (adică, același grafic cu axa orizontală); în fiecare punct următor de curse xi are loc în valoare a probabilității # 957; i. .Naprimer la punctul x1 = 1 este curse # 957; = 1. 0.1 (a se vedea legea empirică a distribuției.); la punctul x2 = 2 este de curse # 957; 2 = 0,2; la punctul x3 = 4 este de curse # 957; 3 = 0,2; etc. La dreapta cea mai mare valoare (x 8 = 13), funcția este egal cu unu. Săgețile de pe capetele punctelor segmente indică faptul că funcția este definită pe intervalele. Cu un volum mare eșantion de elementele sale sunt grupate. Pentru acest interval care conține toate valorile de probă (de la xmin la Xmax), este împărțită în intervale de m disjuncte. Se presupune că intervalul de delimitare dreapta aparține intervalului următor (ultimul interval conține atât frontierele sale). Numărul de intervale t pot fi alese arbitrar sau pentru a găsi formula Sturgess: în care n - mărimea eșantionului. Apoi, lungimea fiecărui interval este egal. unde w - eșantionare domeniul de aplicare. După aceea, frecvența conta nj - numărul de probe care aparțin unui interval de j-a, precum și frecvența acumulate. Rezultatele sunt tabelate frecvența de eșantionare grupate. Procesul formării unui astfel de tabel de frecvență se numește o filă. Desenați frecvența de eșantionare fila din exemplul nostru. Definim numărul de intervale Sturgess prin formula: Numărul m trebuie să fie un număr întreg, și anume, fie 5 sau 6. Deoarece probă interval egal. este mai convenabil de a lua m = 6, pentru că În acest caz, lungimea unui interval. Dacă luăm m = 5, atunci. care nu este foarte convenabil, deoarece Exemple de valori sunt numere întregi. Astfel, despicate valorile intervalelor de eșantionare (1 până la 13), la intervale de timp, în trepte. Rezultatele sunt înregistrate în tabelul (Tabelul 1). În primul număr slot de coloană scriere de la 1 la 6. Apoi, folosind numărul aleatoriu de eșantionare intervale definesc limitele și să le scrie în a doua coloană: 1) cea mai mică valoare de probă este de 1, atunci vom începe să construiască un 1: 1 + 1 → 3 → 2 = 3; 2) 3 → 3 + 2 = 5 → la 5; 3) de la 5 → 5 + 2 = 7 → 7; 4) 7 → 7 + 2 = 9 → la 9; 5) 9 → 9 + 2 = 11 → 11; 6) 11 → 11 + 2 = 13 → 13. Cea mai mare valoare a eșantionului este de 13, înseamnă că intervalele sunt determinate corect. În coloana a treia, scrie mijlocul intervalelor obținute. Intervalul de mijloc (a, b) pot fi găsite prin formula :. de exemplu, pentru intervalul 1-lea; pentru intervalul 2, etc. Intervalul de frecvență de scriere a patra coloană, adică infiltrării frecvenței probelor în intervalul, de exemplu: în intervalul de cădere 1 valori 1 și 2, cu valoarea 1 2 ori întâlnește (n1 = 2) [15]. Valoarea 2 apare de 4 ori (n2 = 4), astfel încât prima frecvență interval este egal; o primă linie de scriere 6; timp de 2 minute valori ale intervalelor cad 3 și 4, în cazul în care valoarea 3 nu se produce în eșantion, o valoare de 4 este găsit de 7 ori (n3 = 7), astfel încât a doua frecvență interval este egal; a doua linie de scriere 7; valori ale intervalelor 3a cad 5 și 6, în cazul în care valoarea 2 găsite de 5 ori (n4 = 2), valoarea 6 este găsit ca de 2 ori (n4 = 2), astfel încât a treia frecvență este egală cu intervalul; o linie de scriere al treilea 4, etc. A cincea coloană a frecvențelor cumulative Tabelul 1 scriere pe principiul: -lea chastotanakopl j. =. (J - 1) + j -lea chastotanakopl -lea chastotaint. De exemplu: frecvența prima stocate este de 6, deoarece frecvență cumulativă anterioară este egal cu 0 (nu este), iar frecvența intervalului 1 este egal cu 6 (a se vedea coloana 4-a.): 0 + 6 = 6; frecvență cumulativă a 2 este egal cu 13, ca prev (I-1) frecvență cumulativă este 6, iar a 2 frecvența intervalului egal cu 7 (a se vedea coloana a 4-a.): 6 + 7 = 13; A treia frecvență cumulativă este egală cu 17, ca prev (2nd) frecvență cumulativă este de 13, iar intervalul de frecvență a treia este 4 (a se vedea coloana a 4-a.): 13 + 4 = 17, etc. În această eșantionare filă de frecvență se termină. Numărul de variație pot fi reprezentate grafic și prin construirea poligon și de prelevare de probe histograma de frecvență. exemplu de imagine grafică pentru a evalua vizual distribuția densității de probabilitate a populației. Pentru a construi un poligon și histograma de eșantionare în acest exemplu utilizează datele conform tabelului 1. Pe plan de coordonate pe axa orizontală reprezintă valorile probă (xi), axa verticală - frecvență (ni) (Fig.2). segmentele individuale ale axelor pot fi diferite (dimensiunea lor este selectată, principiul clarității). Histogramă. La intervale egale cu intervale de tabelul 1 (2a coloana), dreptunghiuri sunt construite cu o înălțime egală cu frecvențele corespunzătoare intervalului (coloana 4-a din tabelul 1). Rezultat set de dreptunghiuri numite histogramă. Poligon. Conectați punctul median al părții superioare a dreptunghiurilor histogramei. Polilinia rezultată se numește o probă de sol (în figura 2 este indicat în roșu). Testarea ipotezei despre legea de distribuție Luați în considerare procesul de testare a ipotezei despre legea de distribuție în exemplul din secțiunea anterioară. Exemplu. Cartea „Winnie the Pooh și toate-toate-toate“ deschise la o pagină aleatoare, în cazul în care puteți selecta un cuvânt aleatoriu. În acest caz, lungimea fixă a cuvântului. Ca urmare a 20 teste se obține eșantionul următor: 4, 1, 4, 5, 1, 13, 4, 10, 2, 4, 7, 2, 2, 4, 6, 4, 5, 6, 2, 4. 1) Se calculează caracteristicile eșantionului: eșantion media, varianța eșantionului, estimare imparțială a varianței. 2) Atunci când nivelul de semnificație # 945; = 0,05 pentru a testa ipoteza că lungimea cuvântul unei distribuții normale. Parametrii de distribuție sunt estimate pe baza unui eșantion: așteptare - prin eșantionarea medie, deviația standard - de rădăcina pătrată a estimării varianței echidistantă. Media eșantionului poate fi găsită prin formula unde k - numărul de diferite unități de probă, n - mărimea eșantionului. O estimare imparțială a varianța: De obicei, caracteristicile eșantioanelor proces de calcul în formă sub forma unui tabel (tabelul 2). In exemplul nostru, k = 8, n = 20, valorile xi și Ni sunt prezentate în numărul eșantion statistic. Completarea tabelul de decontare începe să umple xi și coloanele ni. înregistrarea acestora într-un număr de date statistice. Apoi vom calcula produsul xi · ni și rezultatele sunt înregistrate în a treia coloană. Ultima linie rezumă datele primite 90. Acum, se calculează media eșantionului. împărțirea sumei care rezultă de volumul probei, adică, 20. Acum, calcularea eșantionului mediu, umple coloana a patra, de înregistrare în aceasta corespunde diferenței. de exemplu: Noi scrie prima linie de -3.5; Scriem a doua linie -2,5 etc. În a cincea coloană, coloana precedentă scrie pătrate de valori, de exemplu: Scriem prima linie 12,25; Scriem a doua linie 6.25, etc. Apoi, înmulțim valorile obținute pentru a cincea coloană la frecvența corespunzătoare (a doua coloană), iar rezultatul este scris în ultima coloană, de exemplu: Scriem prima linie 24.50; Scrieți în al doilea 25,00 rând, etc. Ultima linie ultima coloană rezumă datele primite 165.00. Acum vom calcula varianța eșantionului: Am găsit o estimare imparțială a varianței, cunoașterea eșantionului varianța: