fracțiunile Continuare
fracție continuă Capitolul I. DREAPTA finite
§ 1. Reprezentarea numerelor raționale prin fracții continue
§ 2. Fracțiunile corespunzătoare. Proprietățile lor.
Capitolul al II-lea. fracții infinite continuat
§ 1. Introducerea numerelor iraționale reale corecta fracții continuare infinit
1.1. Descompunerea număr irațional reale în fracțiunea continuă infinit corectă.
1.2. Convergență dreapta fracție continuă infinită.
1.3. Unicitatea reprezentării efective a unui număr irațional corecta fracție nesfârșit lanț
§ 2. Aproximarea numărului real de fracții raționale cu un numitor constrângere specificat
2.1. Estimarea de eroare la înlocuirea unui număr real, o fracțiune adecvată.
2.2. Aproximarea numărului real fracțiunilor corespunzătoare
2.3. Teorema Dirichlet.
2.4. Potrivit ca cea mai bună aproximare a fracției
§3. iraționalitate pătratică și fracțiunile periodice au continuat.
§4. Reprezentarea numerelor reale prin fracții continue formă generală.
Scopul muncii mele curs este de a studia teoria fracțiilor continue. În ea, încerc să deschid proprietățile fracțiunilor corespunzătoare, în special extinderea numerelor reale în fracții improprii, erori care apar ca urmare a acestei extinderi, și aplicarea teoriei fracțiilor continue pentru a rezolva unele probleme algebrice.
fracțiunile continue au fost introduse în 1572 de matematicianul italian Bombelli. Desemnarea actuală a fracțiunilor a continuat se găsește în matematician italian Cataldi în 1613. Cel mai mare matematician al secolului al XVIII-lea Leonhard Euler a subliniat mai întâi teoria fracțiilor continue, a ridicat problema utilizării lor pentru rezolvarea ecuațiilor diferențiale, le-a aplicat la descompunerea funcției reprezentate de produse infinite, având în vedere importanța generalizarea acestora.
pe teoria fracțiilor continue de munca a lui Euler a fost continuată de M. Sofronov (1729-1760), academician VM Viskovaty (1779-1819), Daniel Bernoulli (1700-1782), și altele. Multe dintre rezultatele importante ale teoriei se datorează matematicianului francez Lagrange, care a găsit o metodă de soluții aproximative folosind fracții continue, ecuații diferențiale.
Capitolul I. Dreptul continuat finit fracție.
§ 1. Reprezentarea numerelor raționale prin fracții continue.
Un număr întreg care este un divizor al fiecăruia dintre numerele întregi
, Se numește divizor comun al numerelor. divizor comun al acestor numere este numit cel mai mare divizor comun dacă este divizibil cu orice număr de date comune divizor.
- număr rațional, și b> 0. Aplicarea a și b algoritmul lui Euclid pentru a determina cel mai mare divizor comun a obține sistemului final de ecuații:
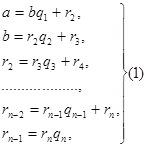
unde coeficientii parțiale ale diviziuni succesive
,
, ...,
numite elemente ale fracției au continuat.
Algoritmul lui Euclid face posibil să se găsească o reprezentare (sau descompunere) a oricărui număr rațional ca o fracție a continuat. Ca elemente ale fracției obținute au continuat caturi parțiale de diviziuni succesive în sistemul de ecuații (1), astfel încât elementele lanțului sunt numite împușcat caturi parțiale. În plus, egalitatea (2) arată că descompunerea într-o fracțiune continuă este alocarea secvențială a se transforma într-o parte întreagă și o parte fracționată.
Ultimul punct de vedere este mai generală decât prima, deoarece este aplicabilă descompunerea unei fracții continuă nu este numai rațională, ci și orice număr real.
Descompunerea unui număr rațional
în mod evident, are un număr finit de elemente, așa cum Nab algoritmul lui Euclid deleniyaa secvențial este finită.
Se înțelege că fiecare fracțiune lanț specific este un număr rațional, adică egală cu un anumit număr rațional. Dar întrebarea nu este dacă există puncte de vedere diferite ale aceluiași număr de fracțiunea rațională a continuat? Se pare că nu există, în cazul în care este necesar să-l facă
.
Teorema. Există unul și numai o fracțiune de lanț finală egală cu acest număr rațional, dar cu condiția ca
.
Dovada: 1) Rețineți că, în caz de eșec al acestei condiții că reprezentarea este eliminată. De fapt, atunci când
:
astfel încât ideea poate fi extinsă:
de exemplu, (2, 3, 1, 4, 2) = (2, 3, 1, 4, 1, 1).
, și așa mai departe; Prin urmare, am ajuns la următoarea concluzie despre poziția reciprocă a fracțiunilor corespunzătoare:
cele mai multe dintre convergents de ordin impar și mai puțin decât toate convergents de ordine, chiar;
2) fracțiunile adecvate de ordine impar formează o secvență ascendentă și ordinea chiar - în scădere (în cazul irațional
aceste secvențe sunt infinite), adică
(În cazul unei raționale
).
-
----
-
---
----
Având în vedere faptul că
, trece la ajuns la concluzia că, în cazul irațional
,
, ... secvență formă de contractare, care, după cum se știe, trebuie să aibă un singur punct comun, care este comună în cadrul secvenței
,
,
Ea aparține tuturor segmentelor de secvență,
și coincide cu punctul menționat, astfel încât
.
Deci, avem următorul rezultat important:
o secvență infinită de convergents
, care rezultă din descompunerea iraționalului
, Ezit despre asta. Sau: real, irațional
egală cu limita fracțiunilor sale de secvențe adecvate Descompunere fracție continuă infinit (selecție proces parțial întreg).
1.2 Convergența dreapta fracțiilor continue infinite.
Noi acum arată că o secvență convergent nu este numai fracțiile adecvate, cum fracțiune continuă infinit, care are loc în timpul descompunerii unui număr irațional
, dar fiecare fracție continuă infinit
- selectate aleatoriu numere întregi pozitive.
Dar pentru aceasta, vom reexamina poziția relativă a fracțiunilor corespunzătoare.
În acest scop, ia în considerare formula:
care sunt valabile pentru orice fracțiune continuă infinit.
1. Formula (1) arată că orice fracțiune adecvată chiar comanda mai mare decât două fracțiuni corespunzătoare învecinate a căror ordine este una sau mai puțin decât, adică
în stânga
,
Acest lucru desigur, arată importanța fracțiilor continue în matematică.
Ele pot fi aplicate cu succes la soluția de ecuații de forma ax + nedeterminate prin = c. Principala dificultate în rezolvarea unor astfel de ecuații este de a găsi o parte din soluția sa specifică. Deci, cu ajutorul fracțiilor continue poate fi un algoritm pentru a găsi această soluție specială.
fracții Continuare pot fi aplicate ecuații nedeterminate mai complicate, de exemplu, ecuația așa-numita lui Pell:
(
).
fracțiuni cu lanț fără sfârșit pot fi utilizate pentru rezolvarea ecuațiilor algebrice și transcendente pentru calcul rapida a valorilor anumitor funcții.
În prezent, fracțiunile continuat sunt tot mai folosite în tehnologia de calculator, deoarece permite construirea unor algoritmi eficienti pentru a rezolva o serie de probleme pe computere.
1. MB Balk, GD Balk. Math după școală. M, "Educație" 71.
2. AA Buchstab. Teoria numerelor. M, "Educație" 96.
3. Algebră și teoria numerelor. Editat de N. Vilenkin, M, "Educație" 84.
4. IM Vinogradov. Bazele teoriei numerelor. M, "Știința", 72.
5. AA Kocheva. Cartea de probleme în algebră și teoria numerelor. M, "Educație" 84.
6. LY Kulikov, AI Moskalenko, AA Fomin. Probleme în algebră și teoria numerelor. M, "Educație" 93.
7. ES Lyapin, AE Evseev. Algebră și teoria numerelor. M, "Iluminismul", 74.
8. matematică Encyclopedia, volumul V, M, "Enciclopedia sovietică", 85.
9. Sh.Kh. Mihelovich. Teoria numerelor. M, "High School" 67.