Formulele și proprietățile dreptunghiuri

H născut înainte de studenți și tutori în matematică și pot găsi proprietățile de bază și formulele patrulatere pătrate, studiate în școală a programului principal. folosesc în mod regulat aceste cunoștințe teoretice despre subiect și examinați lecțiile de geometrie (geometrie plană) și în curs de pregătire pentru examen în matematkie. Toate conceptele matematice și fapte sunt ilustrate cu o culoare care să evidențieze principalele caracteristici studiate.

1) dreptunghiuri pătrate

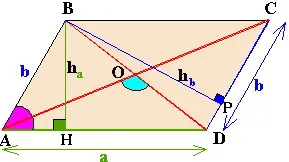
bază de produse și înălțimea

părți poroizvedenie prin sinusul unghiului dintre ele

diagonalele poluproizvedenie din sinusul unghiului dintre ele

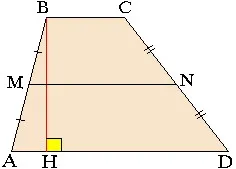
lucra pe jumătate suma înălțimii bazelor

produsul din înălțimea liniei mediane

diagonalele poluproizvedenie din sinusul unghiului dintre ele

Zona oricărui patrulater

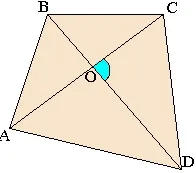
Zona unui patrulater arbitrar poluproizvedeniyu diagonalele sale egale cu sinusul unghiului dintre ele

2) Proprietățile paralelogramului

Paralelogramul:
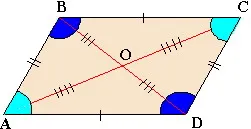
laturile opuse și unghiuri sunt egale

diagonalele se intersectează în punctul de intersecție și bisect

3) Suma pătratelor diagonalele unui paralelogram este egal cu suma pătratelor laturilor, adică,

3) Media în linia de trapez

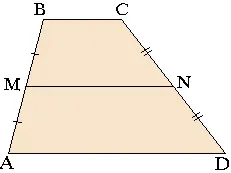
Teorema pe linia de mijloc: linia de mijloc paralelă cu bazele trapezului și este egală cu jumătate din suma acestora.
Asta este,

4) Linia medie este un trapez isoscel

Midline în trapez isoscel este egală cu baza inferioară a segmentului de conectarea bazei la partea superioară a înălțimii colmatare atras de ea.

5) Teorema pentru a comuta pe diagonală trapez

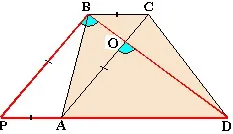
Teorema: Dacă trapez prin partea de sus B, așa cum se arată în partea stângă. efectueze o secțiune paralelă a unuia dintre diagonalele, acesta va deveni realitate următoarele fapte:

Keystone - isoscele isoscel

6) Patru punct remarcabil în trapezului

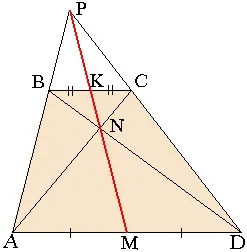
Teorema: În orice punct de intersecție a diagonalelor trapezului, punctul peersecheniya și părți urmari mijlocul motivelor se află pe o singură linie.

Acesta este punctul de M, N, K și P sunt coliniari

Kolpakov Aleksandr Nikolaevici. Math tutore.

Alexander, desigur, există o mulțime de ghiduri de buzunar, DAR! Ar fi cool să facă pentru tutori în matematică materiale descărcate în orice format convenabil, precum și cu privire la anumite sarcini de la o astfel de foaie de ieftin din nou de la simplu la complex.

Această selecție bună, în opinia mea, lipsa de informații cu privire la colțuri, de exemplu, două unghiuri interne ale unui paralelogram, conectat pe de o parte adăuga până la 180 de grade.

În principiu, dacă formula în pătrat în diagonală peste ea pentru a lua un unghi mai mic între ele? Sau poate cineva?

Alexander, dacă nu chiar mai dificil, ar place pentru a obține un fișier la e-mail sau tyknut mondială de referință la acesta. Pentru mai devreme foarte recunoscător pentru sarcina titanică.