Formula intensității câmpului magnetic în Fizică

Definiția și câmpul magnetic formula

intensitatea câmpului magnetic este o mărime fizică vector, dirijat tangențial la liniile de forță, ceea ce este caracteristic unui câmp magnetic egal cu:

în care - vectorul inducție magnetică, H / m (N / A 2) - o constantă magnetic, - vectorul magnetizării în mediul de testare la teren.

Pentru un câmp magnetic într-un intensitatea câmpului magnetic în vid este dată de:

Într-un mediu izotrop, formula (1) este convertit în forma:

în care - cantitatea scalară numită permeabilitatea magnetică relativă a mediului (sau permeabilitatea magnetică). Într-un mediu izotrop, vectorii de câmp magnetic de inducție magnetică și aceeași direcție.

Uneori, intensitatea câmpului magnetic este definită ca fiind cantitatea vector, direcționată tangențial la linia de câmp de forță, modulo egală cu raportul dintre forța (dF), câmp care acționează asupra unui singur element al curentului (dl), care este dispus perpendicular pe câmp în vid, la o constantă magnetic:

Biot-Savart-Laplace

Aceasta este cea mai importantă lege în electromagnetism. Ea determină vectorul intensitate la un punct arbitrar al câmpului magnetic, care creează un vid în elementar dl lungime conductor cu un curent I constant:

în care - elementul conductor vector care modulo egală cu lungimea conductorului, direcția coincide cu direcția curentului; - raza vectorului, care este purtat de conductorul la punctul elementar considerat considerând domeniu; .

Vector - perpendicular pe planul în care vectorii sunt și este direcționat astfel încât capătul vectorului său de rotație pe calea cea mai scurtă pentru a se alinia cu vectorul a avut loc în sens orar. Pentru a găsi vectorul de direcție poate fi folosit regula din dreapta (Gimlet (șurub) este rotit, astfel încât mișcarea sa înainte coincide cu direcția actuală, apoi direcția în care mânerul se rotește șurubul, coincide cu direcția câmpului vectorial, care creează current).

Biot-Savart-Laplace face posibilă calcularea magnitudinea intensitatea maximă a câmpului magnetic, care creează un curent care curge printr-un conductor de orice formă.

Pentru a găsi intensitatea deplină a câmpului magnetic, care creează un punct în curentul de test I, care curge prin conductorul l, vectorul ar rezuma toate tensiunile elementare generate de elementele conductoare și rezultă din formula (4).

unități de măsură

Unitatea de bază a momentului de forță în unități SI este: [H] = A / m

Exemple de rezolvare a problemelor

Sarcină. Care este tensiunea (H) în centrul unei bobine circulare (R - raza de rotire) cu un curent I.

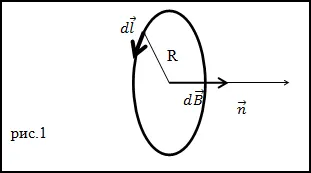
Decizie. Fiecare curent bobina elementar un câmp magnetic în centrul cercului, al cărui intensitate este direcționată de-a lungul normal pozitiv la planul buclei bobinei (Figura 1). De aceea, dacă o intensitate a câmpului elementar găsită de Biot-Savart - Laplace, adăugarea vectorială a câmpurilor elementare vor fi înlocuite cu algebric.

În conformitate cu legea Biot-Savart - Laplace dH este egal cu:

Folosind expresia (1.1), în cazul nostru, obținem:

Ia de-a lungul unui contur integrală, obținem:

Sarcină. Care este câmpul magnetic, ceea ce creează un electron se deplasează uniform cu viteza v? Dacă punctul în care este cercetat câmpul, se află la o distanță r de un electron pe perpendiculara pe vectorul viteză, dacă perpendicular naviga prin poziția instantanee a particulei.

Decizie. Fă un desen.

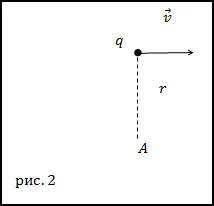
Câmpul magnetic va fi urmărit prin aplicarea legii Biot - Savart - Laplace:

În cazul în care toate taxele sunt aceleași (q), atunci densitatea de curent este egal cu:

sarcină negativă, deci, vectorii de direcție sunt opuse. n - concentrația de încărcare. Înlocuim (2.3) la (2.2), rezultatul în (2.1) obținem:

unde dN = Sdln - numărul de particule încărcate în dl interval. În acest caz, intensitatea câmpului, care generează o singură încărcare:

Potrivit problemei. intensitatea medie a modulului câmpului magnetic la punctul A (Figura 2) va fi: