Formula de argument dublu

§ 24. Formula dublu argument

Aici ne vom concentra asupra formulelor de trigonometrie, ne permite să-și exprime aceste formule se numește de obicei argumentul dublu. Numele poate fi, nu este foarte bun, așa cum, într-adevăr, și nume precum „formulă pentru a aduce“, „sumă sine“, „cosinusul diferenței“, etc, dar nu contează: principalul lucru pe care există un simbol verbal permițând dedicat pentru a înțelege ceea ce este în joc.
Să considerăm sin2h expresie, depunerea cu 2 sub forma x + x. Acest lucru va permite să aplice păcatul expresie (x + x) formula "sumă sine" (a se vedea. § 21). Avem:

Să considerăm sos2h expresie, depunerea cu 2 sub forma x + x. Acest lucru va permite să se aplice cos de expresie (x + x) formula "sum cosine" (a se vedea. § 21). Avem:

Să considerăm expresia tg 2, prezentând în același timp, sub formă de 2 x + x. Acest lucru va permite să aplice tg expresie (x + x) formula "sumă tangent" (a se vedea. § 23). Avem:

Formula „argument sinus dublu“ și „cosinus dublu argument“ valabil pentru orice valori argument (fără restricție), în timp ce formula „dublu argument tangent“ valabil numai pentru acele valori ale argumentului x, care sunt definite tg x și tg 2 X și De asemenea, numitor nenul, și anume,
Desigur, formula argument dublu poate fi aplicat și în cazul în care poziția argumentului x ia o expresie mai complexă. Astfel, următoarele relații:

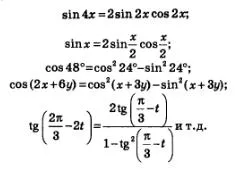
Și, ca întotdeauna, oricare dintre cele trei rezultate obținute în această secțiune, formulele de argumentare dublu poate fi folosit ca o scriere de la dreapta la stânga și de la stânga la dreapta. De exemplu,

Exemplul 1. Dovedește identități:

Soluție: a) utilizarea faptul că 1 x = sin 2 + cos 2 x, formula sinusul dublu argument. obținem:

Exemplul 2. Reducerea fracției
Decizie. Utilizarea numărătorul dovedită în exemplul 1 și identitatea și numitorul - argument double cosinus formula. obținem:

Exemplul 3. Calculați:
Soluție: a) exprimarea Specification reprezintă partea din dreapta a argumentului cosinus dublu. Văzând acest lucru, obținem

b) Expresia set este în partea dreaptă a dublei sinusul argumentului, dar nu are numai multiplicatorul 2. Introduceți-l, obținem:

c) Acest exemplu este mult mai dificil, dar este mult mai frumos decât anterior: este necesar să se ghicească înmulțirea și împărțirea expresia dată la 4sos18 °. Ce va da? A se vedea:

După cum puteți vedea, am folosit de două ori cu formula de sine a argumentului dublu. Pentru a aduce calcul la final, observăm că 72 ° = 90 ° -18 °. Deci, păcatul 72 0 = sin (90 ° -18 0) sos18 = 0. Astfel,

Exemplul 4 Pentru a dovedi identitatea
Decizie. Transformarea în partea stângă a identității este obligatorie:

Multiplicarea atât numărătorul și numitorul ultimei fracțiunii 2 ( „personaliza“ numitorul formulei de sinusul dublu argumentul), obținem:

Deci, ceea ce ne-am dorit să dovedească.
Notă. Încă o dată Vă atrag atenția asupra faptului că identitatea a fost dovedită numai pentru valoarea admisibilă a lui x, mai precis pentru
pentru valorile lui x pentru care numitorilor disponibile sunt non-zero.
Exemplul 5. Știind că

Soluție: a) folosește formula x 2 + sin cos 2 x = 1. Avem:

b) Pentru a calcula utilizarea sin2h formula păcatul 2 = sin 2 hsoz x.
Pentru că x valoare dată în stare, iar valoarea lui x păcat găsi urmează. În primul rând, știm că
În al doilea rând, cu condiția x argumentul aparține al patrulea trimestru, și sinus este negativ. Acest lucru înseamnă că, dintre cele două valori

c) tg2h calculată folosind definiția tangentei:

g) calcularea primei utilizări pentru conducere formula:
Se aplică formula la expresia soz4x argumente cosinus duble soz4h 2 = cos 2 - sin 2 2. Noi folosim faptul că valorile cos 2 și 2xuzhe păcat ne-a găsit:

Exemplul 6. Rezolva ecuația sin4h-soz2h = 0.
Decizie. Dacă în partea stângă a ecuației aplicată expresiei sin4x formula sine argument dublu, acesta va fi capabil să se extindă în partea stângă a factorizarea. Avem în mod constant:

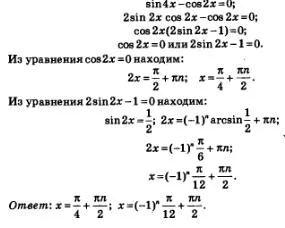
AG Mordkovich Algebra Grad 10

Dacă aveți corecturi sau sugestii la această lecție, vă rugăm să ne contactați.

Dacă doriți să vedeți alte ajustări și sugestii pentru lecții, uita-te aici - Forumul Educațional.