Formula accelerare fizica

Accelerația (accelerația instantanee) este vectorul care definește viteza cu care se schimbă în mișcare a vitezei punctului material.

De obicei denota accelerare. În mecanica teoretică întâlnește desemnarea accelerare :. Definirea matematică a accelerației instantanee este expresia:

în cazul în care - viteza de deplasare a unui punct material

în care - raza - vectorul care definește poziția unui punct material în spațiu.

vector Acceleration este situat în planul de contact în care principal este normal și tangenta la traiectoria, deci are o direcție spre traiectoria concav.

Unitati de masurare de accelerare

Principalele unități ale unei accelerare în unități SI este: [a] = m / s 2

tipuri de accelerare

Dacă vom construi avionul osculating în orice punct al traiectoriei, vectorul este descompus în două componente perpendiculare:

unde - un vector direcționat de-a lungul normala la un important centru de curbură a traiectoriei punctului material - aceasta este o accelerație normală; - vector direcționat de-a lungul tangentei la calea - este accelerația tangențială. În acest caz, următoarele ecuații dețin:

în care - amplitudinea vitezei, R - raza de curbură a traiectoriei, un - vector proiecție pe versorul principal normale AT - vector proiecție pe tangenta vectorului unitate. Valoarea unei determină viteza ratei de a schimba direcția și amploarea AT - rata de schimbare a vitezei modulului.

Dacă există o astfel de mișcare se numește uniformă. mișcarea Pria_ este ravnoperemennym (la ravnozamedlennym în mod uniform accelerată).

accelerația medie în intervalul de timp de la punctul de material se numește o cantitate vectorială, egal cu raportul:

În cazul în care limita accelerația medie coincide cu accelerația instantanee:

Formula accelerare în diferite sisteme de coordonate

Coordonatele carteziene ale proiecției accelerației (ax, ay, az) pe axa (X, Y, Z) poate fi reprezentat ca:

unde - vectorii unitare ale axele X, Y.Z. În această accelerare modul este:

Într-un sistem de coordonate cilindric, avem:

In modulul de coordonate sferice de accelerare a sistemului poate fi definit ca:

Exemple de rezolvare a problemelor

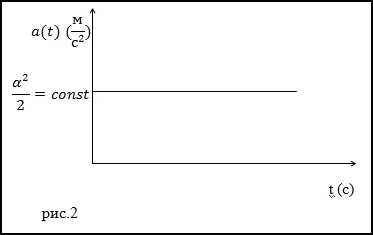
Sarcină. Materialul se deplasează de-a lungul circumferinței (fig.1), care are o rază R = 2m, ecuația de mișcare, secunde gdetv și S în metri. Ce modul de accelerare care indica la t = 3 c?

Decizie. Ca bază pentru rezolvarea problemei cu ajutorul formulei:

Folosind o ecuație predeterminată de mișcare, obținem modulul vitezei punctului material:

Diferențierea ecuația (1.2) viteza modulului în raport cu timpul obținem componenta tangențială a accelerației:

Pentru calcularea componentei normale a vitezei punctului material al mișcării noastre ar trebui să fie folosind expresia (1.2) pentru a găsi:

Folosind expresia (1.1) se calculează accelerația dorită:

Sarcină. Care este dependența de accelerare a punctului material al timpului (a (t)), în cazul în care se deplasează de-a lungul axei de particule X a și viteza acestuia variază în conformitate cu ecuația: unde - constantă mai mare decât zero? La momentul inițial (la t = 0 s), punctul de material se află la originea (x = 0 m). Desenați programa o (t).

Decizie. pot fi scrise de condițiile problemei, că:

Folosind formula (2.1), descoperim dependența coordonatele xot de timp (x (t)):

în cazul în care constanta de integrare poate fi găsită de condițiile inițiale ale problemei. Știm că x (0) = 0, atunci C = 0. Avem:

Folosind formula pentru găsirea uskoreniyadlya cazul nostru (mișcarea de-a lungul axei X):

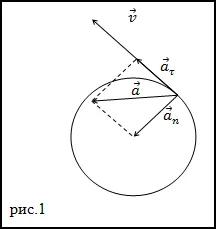
obținem expresia dorită pentru o (t):

Răspuns. accelerare nu depinde de timp, atunci programa o (t) ia forma (Fig.2).