Exemple de utilizare a coordonatelor cilindrice și sferice

Ca și în trecerea la coordonate polare în dublu integrala, da o rețetă certă atunci când a folosi coordonate cilindrice sau sferice, nu putem, este o chestiune de experiență. Puteți încerca să utilizați coordonate cilindrice, în cazul în care integrandul și / sau ecuații ale suprafețelor care limitează cantitatea de $ \ mathbf> $, în funcție de combinația de $ \ mathbf> ^ + \ mathbf> ^ = \ mathbf> ^<2>$; sferic - în cazul în care aceste ecuații depind de $ \ mathbf> ^ + \ mathbf> ^ + \ mathbf> ^ = \ mathbf> ^<2>$. Luați în considerare câteva exemple.

Găsiți suma de $ \ mathbf> $ totalul celor două bile, zone restricționate

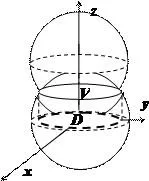
Intersecția sferelor este situat la $ 2RZ = R ^ 2 \ rightarrow z = R / 2 și $ este un cerc de rază R $ \ frac $. Volumul de $ \ mathbf> $ este mărginită de deasupra suprafeței de $ z = \ sqrt $, sub - suprafața de $ z = R- \ sqrt $. Calculele în coordonate carteziene dat $ V = \ iiint \ limits_V = \ iiint \ limits_V = \ int \ limite _> ^> R ^ 2-x ^ 2 >> ^ R ^ 2-x ^ 2 $ >>> >>> ^ - calcule destul de greoaie.

În formă cilindrică coordonează suma de $ \ mathbf> $ este mărginită de mai sus $ suprafața z = \ sqrt $, sub - suprafața de $ z = R- \ sqrt $, deci

În coordonate sferice, sfera ecuației de jos devine $ r = R $, de sus - $ r ^ 2 = 2Rr \ cos \ theta \ rightarrow r = 2R \ cos \ theta $, intersecția lor corespunde valorii $ \ cos \ theta = 1/2 \ rightarrow \ theta = \ pi / 3 $. În intervalul de $ 0 \ leqslant \ theta \ leqslant \ pi / 3 \ quad \ mathbf> $ variază de la $ 0 $ la $ \ mathbf> $, în intervalul de $ \ pi / 3 \ leqslant \ theta \ leqslant \ pi / 2 \ quad \ mathbf> $ variază de la $ 0 $ la $ 2R \ cos \ theta $, deci

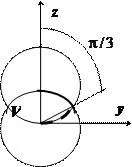
In acest exemplu, complexitatea calculelor în coordonate cilindrice și sferice aproximativ aceeași.

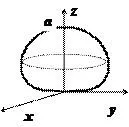
Se calculează volumul corpului delimitat de suprafața $ \ stânga (\ dreapta) ^ = a ^ 3z, \ a = const> 0 $

Se calculează integral $ \ iiint \ limits_U + 2 +> \ dreapta) DXDYDZ>, $ unde regiunea (U) este limitată de către suprafața (+ \ le 1) și planul (z = 0,) (z = 1).

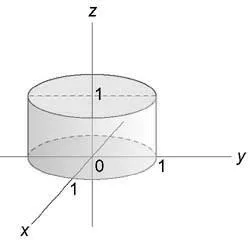
Acest lucru este convenabil pentru a calcula integralei în coordonate cilindrice. Aria de proiecție a integrării pe planul (Oxy) este un cerc (+ \ le 1) sau (0 \ le \ rho \ le 1).

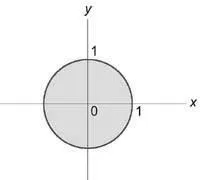
Apoi integrala este egal cu $ I = \ int \ limits_0 ^ \ int \ limits_0 ^ 1 \ rho d \ rho> \ int \ limits_0 ^ 1 $

Aici, în al doilea factor adăugat integral (\ rho) Jacobian transformării coordonatelor carteziene în formă cilindrică. Toate cele trei integralei pentru fiecare variabilă sunt independente una de cealaltă.

Se calculează $ integral \ iiint \ limits_U +> \ dreapta) DXDYDZ>, $ unde regiunea (U), delimitată de suprafețele (+ = 3z,) (z = 3)

Integrarea Zona este reprezentată în Figura

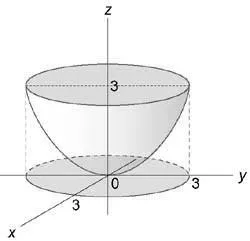
Pentru a calcula rândul său, parte integrantă a coordonate cilindrice: $ \; \; \; \; $ Differential este egal deci $ DXDYDZ = \ rho d \ rho d \ varphi dz \; \; \ stânga (> \ dreapta) $.

Ecuația de suprafață parabolică ia forma: $ \ varphi + \ varphi = 3Z \; \; \ textul \; \; = 3z. Regiune integrare $ proiecție (U) pe plan (Oxy) este un cerc (+ \ le 9) o rază (\ rho = 3).

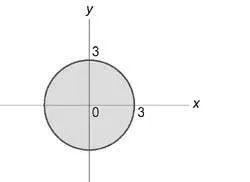
Coordonate (\ rho) și variază de la (0) până la (3), unghiul (\ varphi) din (0) până la (2 \ pi) și coordonate (z) de (\ mari \ frac >> \ normalsize) la ( 3.)

Folosind coordonatele cilindrice, găsiți valoarea $ integrală I = \ int \ limits_<- 2>^ 2 \ int \ limits_<- \sqrt>> ^ >> \ int \ limits_0 ^ -> dz> $

Regiunea de integrare (U) este prezentată mai jos:

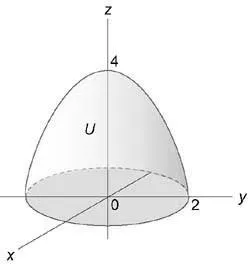
proiecția sa pe planul (Oxy) este un cerc (+ =):

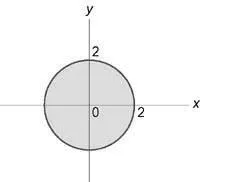
Se calculează coordonatele integrant folosind cilindric: $ \ iiint \ limits_U +> DXDYDZ> $ Zona (U) este limitată de paraboloidului (z = 4 - -,) cilindru (+ = 4) și avioanele (y = 0,) (z = 0. )

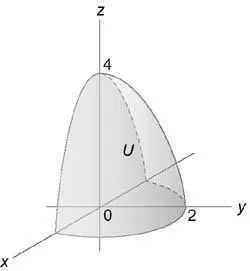
Reprezentând schematic regiunea de integrare (U,), descoperim că proiecția pe planul (Oxy) este raza semicercului (\ rho = 2).

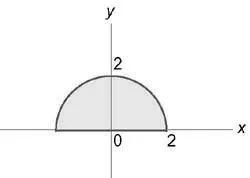
Găsiți $ integral \ iiint \ limits_U, $ în cazul în care regiunea (U) este delimitată de planuri (z = x + 1) (z = 0) cilindrice și suprafețe (+ = 1) (= + 4)

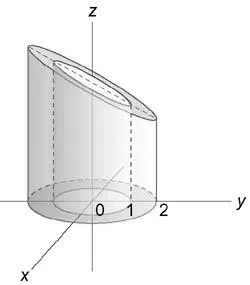
Calculăm integrala în coordonate cilindrice. Din starea de $ 0 \ le z \ le x + 1 $ care $ 0 \ le z \ le \ rho \ gama cos \ varphi + 1. $ de integrare în planul (Oxy) este un spațiu inelar delimitat de cercuri (+ = 1) și (= + 4)

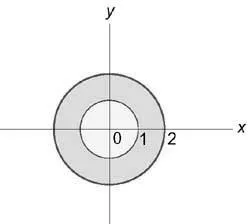
Prin urmare, variabile (\ rho) și (\ varphi) variază în intervalul de $ 1 \ le \ rho \ le 2 \, \, 0 \ le \ varphi \ le 2 \ pi $.

Acest rezultat este logic deoarece regiunea (U) este simetrică față de un plan (Oxz,) și funcția integrandul este chiar.

Găsiți integral (\ iiint \ limits_U + +> DXDYDZ>), unde regiunea de integrare (U) cu bile, dată de ecuația (+> = 25.)

Deoarece regiunea (U) este o sferă, și, de asemenea, integrandul este o funcție care depinde de $ f \ left (+ +> \ dreapta), $ apoi trece la coordonate sferice.

Calculați integrală $ \ iiint \ limits_U + +> \ dreapta)> ^ >>>> DXDYDZ>, $ în cazul în care regiunea (U) este bila unitate (+ +> \ le 1.)

Centrul sferei se află la originea. Prin urmare, în coordonate sferice din regiunea de integrare (U) descrie inegalitățile $ \; \; \; \; $

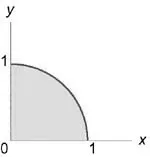
Se calculează integral (\ iiint \ limits_U), unde regiunea (U) este o parte a bilei (+ + \ le,) dispus în primul Octant (x \ ge 0, y \ ge 0, z \ ge 0.)

Calculați integrală $ \ int \ limits_0 ^ 1 \ int \ limits_0 ^ >> \ int \ limits_0 ^ - >> + +> \ dreapta)> ^ 2> dz>, $ folosind coordonate sferice.

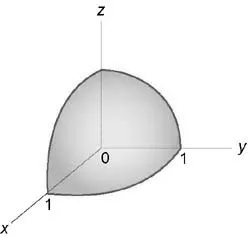
Integrarea Zona face parte din mingea situat în primul Octant și, prin urmare, inegalități limitate $ \; \; > \; \; .> $

A se vedea, de asemenea:

Calculul suprafață

Clasa $ S $. Teorema de clasa zamknytosti $ S $

Proprietăți triple integrantă

Clasa M. Teorema privind clasa M este închisă

Du-te la conținut $ \ rightarrow \ rightarrow \ rightarrow $