energie câmp magnetic - studopediya
10. Bobina 20 cm lungime și 4 cm în diametru are o bobina cu trei straturi dense de sârmă 0,1 mm în diametru. Prin înfășurarea sărată Ida curge curent 0.1 A. Dependență = f (H) pentru materialul de miez prezentat în Fig. 10. Se determină tensiunea și câmpul de inducție în sare-Noida, permeabilitatea magnetică a miezului, inductanța bobinei, solenoid în vrac densitatea de energie și de energie câmp.
Decizie. Câmpul din interiorul solenoidului poate fi considerat NYM omogen. În acest caz, intensitatea câmpului electromagnetic este egal cu: unde I - curentul din înfășurarea, - numărul de spire pe unitatea de lungime a solenoid, k - numărul de straturi de înfășurare, d - diametrul firului. atunci
Conform schemei B = f (H) (Fig. 10) locat-Dim că tensiunile de 3000 A / m, cu inducție-sponds până la 1,7 Tesla. link Execu-Zuya între inducție și intensitate a câmpului, de exemplu, definesc permeabilitatea magnetică:
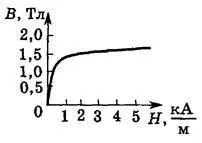
Fig. 10 unde l - lungimea solenoidului,
- aria secțiunii transversale a solenoidului.
Având în vedere faptul că. obținem:
Densitatea în vrac a energiei câmpului magnetic:
Energia câmpului magnetic al solenoidului: sau
Substituind date numerice, obținem:
11. Curentul din creșterile electrovalve uniform de la 0 la 10 A per 1 minut. în timp ce solenoid acumulează energie 20 J. Ce emf este indus în solenoid?
Decizie. Energia câmpului magnetic al solenoidului cu inductanță L. suprafață prin care un curent curge I. este egal cu: unde
EMF induse de auto care apar în solenoid atunci când curentul în bobina sa la un moment dat # 916; t, este:
12. Un singur strat bobina, fără o lungime de bază de 20 cm și dia-metru
4 cm are un fir dens din cupru de înfășurare cu diametrul de 0,1 mm. 0.1 s amperaj scade uniform în acesta de la 5 la 0. A divide Oprah EMF autoindusă în solenoid.
Decizie. Auto-inducție forță electromotoare care apare atunci când actuala schimbare SRI # 916; I în timpul solenoid # 916; t.
Inductanța bobinei este egală cu:
unde # 956; 0 - constanta magnetic;
n - numărul de spire pe unitatea de lungime a solenoidului
(Cu înfășurare etanșă);
l - lungimea solenoidului;
- aria secțiunii transversale a solenoidului;
D - diametrul unui solenoid, # 956; = 1.
12. Bobina solenoid are o rezistență de 10 ohmi. Ceea ce este a lui în inductivitatea, în cazul în care curentul de trecere de 0,05 este alocată o cantitate echivalentă de energie termică la energia câmpului magnetic sare-Noida?
Decizie. energia câmpului magnetic al solenoidului este egal cu:
Cantitatea de căldură Q este determinată de Joule - Len-CA:
Conform legii conservării energiei
În cazul în care este inductanța
13. Într-un plan perpendicular pe câmpul magnetic încordate-Ness
2 # 8729; 10 5 A / m, se rotește tija de lungime 0,4 m în jurul unei axe care trece prin mijlocul acesteia. Tija este indusă forță electromotoare de 0,2 V. Pentru a determina viteza unghiulară a tijei.
Decizie. emf indusă este egală cu rata de schimbare a fluxului-mag netic # 934;, intersectate de bază în rotație:
în care - inducția magnetică;
dS - zona traversată de tija în rotație cu o viteză unghiulară # 969;.
Jumătate din tijă, având o rază. , Prin rotirea printr-un unghi d # 966; traversează zona. și întreaga tijă traversează zona.
14. Un miez solenoid (# 956 = 1000) 15 cm lungime și 4 cm în diametru are 100 se întoarce la 1 cm lungime și încorporate în circuitul de sursa de curent. tărie 1 ms curent schimbat la 10 mA. Pentru a determina forța electromotoare auto-inducție, presupunând că curentul în circuit variază uniform.
Aceasta este dată de: l = 0,15 m; D = 0,04m; n = 10 4 m -1; # 956; = 1000; # 916; I = 10 -2 A;
Decizie. EMF induse de sine este egală cu:
Inductanța bobinei este dată de:
15. La capetele aripilor aeronavelor cu o scară de 20 m, de zbor la o viteză de 900 km / h se induce emf 0,06 V. Se determină componenta verticală a câmpului magnetic Terr-li.
Decizie. Pilotarea aeronavei traversează câmpul magnetic terestru a cărui intensitate H este legată de inducție în co-relația. emf indus care rezultă în acest caz, este egală cu rata de schimbare a fluxului magnetic F traversat de aripile avionului, S = BS.
În timpul plan dt traversează zona.
16. Două condensatoare cu capacitances 0,2 microfarazi și 0,1 microfarazi conectate în serie într-un circuit de tensiune de curent alternativ de 220 V și frecvența de 50 Hz. Găsiți curentul în circuit și căderea de tensiune pe primul și al doilea condensator.
Având în vedere: C1 = 0,2 microfarazi = 2 # 8729, iulie 10F; C2 = 0,1 uF = 1 # 8729, iulie 10F; U = 220 V; = 50 Hz.
Soluție: capacitatea condensatorului este exprimată prin formula:
unde (2) - oscilații de frecvență ciclică. Substituind ecuația (2) în (1), vom găsi rezistență condensatori:
Din moment ce condensatoarele sunt conectate în serie, rezistența lor totală este dată de:
În conformitate cu legea lui Ohm pentru curent alternativ. (4)
unde (5) și (6) - valorile efective ale curentului și tensiunii. Substituind (3) în (4) cu (5) și (6) găsim curentul în circuit:
Potențiala scădere de la primul și al doilea condensator, respectiv, va fi :; .
; Să înlocuiască valorile numerice: B și
; Substitut valorile numerice
Tensiunea 17. Circuitul de curent alternativ de 220 V și 50 Hz în serie condensator este 35.4 microfarazi, 100 ohmi și o bobină de inductanță 0.7 Gn. Găsiți curentul în circuit.
Dată fiind: C = 35,4 # 8729; 10 -6 F; U = 220 V; = 50 Hz; R = 100 ohmi; L = 0,7 Gn.
Soluție: Conform legii lui Ohm pentru curent alternativ, intensitatea curentului dat de expresia (1), în care (2) - Circuit de impedanță; (3) și (4) - valorile efective ale curentului și tensiunii. Substituind ecuația (2) în (1), și utilizând acid (3) și (4), obținem:
. Să înlocuiască valorile numerice:
18. 22.6 bobina mH Inductanța și rezistența R inclusă în paralel cu circuitul de curent alternativ cu o frecvență de 50 Hz. Găsiți rezistență în cazul în care se știe că defazajul între tensiune și curent 60 0.
Dată de: L = 22,6 = 22,6 mH # 8729; 10 -3 Gn; = 50 Hz; 60 = 0.
Soluție: Dacă inductanța și rezistența sunt incluse în paralel cu circuitul de curent alternativ, defazajul între tensiune și curent se determină prin formula (1). unde (2) - oscilații de frecvență ciclică. Substituind ecuația (2) în (1) randamentele :. în cazul în care ne exprimăm rezistența :. Să înlocuiască valorile numerice: