Energia potențială în intensitatea câmpului extern

Din expresia (4.9) rezultă că lucrarea este egală cu creșterea funcției potențial, iar această lucrare se duce la incrementarea energiei cinetice a particulei, așa cum arată (4.5). Astfel,

Vom trece de la o funcție. asociată cu raportul

Apoi, din (4.11), obținem :. sau.

Acest rezultat înseamnă că valoarea pentru particula în domeniul forțelor conservatoare, rămâne constantă, adică Este o constantă de mișcare. Funcția se numește energia potențială a unei particule într-o intensitate a câmpului extern. Astfel, energia potențială caracterizează interacțiunea particulei cu intensitatea câmpului electromagnetic și depinde de poziția particulei în acest domeniu, și anume coordonatele.

Valoare. egală cu suma de energie cinetică și potențială, numită energia mecanică totală a particulei.

Din expresia (4.9) cu (4.12), obținem

-lucrările efectuate pe teren conservatoare forțe ale particulelor egală cu diminuarea energiei potențiale a particulei, adică de lucru se face în detrimentul potențialelor rezerve de energie. Activitatea desfășurată de forțele conservatoare în tranziția de la sistemul de o anumita pozitie la zero se numește potențialul energetic U a sistemului în această poziție.

Expresia (4.7) cu (4.12) ia forma

silil, care acționează asupra particulei în intensitatea câmpului staționar este egal cu gradientul energia potențială a particulei în acest domeniu, luat cu semnul opus.

Să alta decât câmpul potențial staționar al forțelor, de asemenea, acționează forța de non-conservatoare particula. Apoi, în timpul tranziției particulei de la punctul 1 la punctul 2 de mai sus se va face de lucru în care - lucrează forțe non-conservatoare. Activitatea forțelor conservatoare egală cu scăderea energiei potențiale. atunci

Activitatea totală a tuturor forțelor aplicate particulei este în creștere de energie cinetică. sau

-activitatea forțelor non-conservatoare este cheltuit pe incrementarea energia mecanică totală a particulei.

Energia potențială, precum și funcția de potențial este definit până la o constantă aditiv arbitrar. Cu toate acestea, acest lucru nu contează, din moment ce toate funcțiile incluse într-un potențial valori diferența de energie, sau derivați ai acestora. În fiecare sarcină special, este selectat originea energiei potențiale, care sunt de calculare a energiei în alte poziții. Prin urmare, poate avea valori atât pozitive, cât și negative.

Forma particulară a funcției depinde de natura câmpului de forță. În domeniul gravitației. care este măsurată de la un nivel arbitrar.

Să considerăm un sistem care constă din particule care nu interacționează în domeniul forțelor conservatoare. Fiecare particulă are o energie cinetică și potențială a numărului de particule, atunci putem scrie pentru fiecare particulă

Însumând aceste expresii pentru toate particulele obține

- energia mecanică totală a sistemelor de particule care nu interacționează, care acționează numai forțe conservatoare, rămâne constantă.

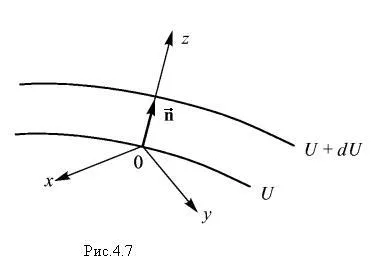
Pentru a clarifica sensul gradientului geometric este utilă introducerea suprafețele echipotențiale. adică aceste suprafețe pe care funcția scalară U rămâne constantă: U (x, y, z) = const.

Fie U - una dintre aceste suprafețe și lăsați să treacă prin punctul O. spațiul care este definit de gradient (Figura 4.7.). Punem la acest punct de origine. axa Z este îndreptată de-a lungul normalei la suprafață (- vector unitate normală), iar axele X și Y se află într-un plan tangent la suprafața în punctul O. Prin urmare, în primă aproximație, de-a lungul axelor x și y U nu modifică funcția :. Prin urmare, din moment ce, în acest caz, =. Dacă U este crescută în direcția axei Z. ∂ U / ∂ z> 0 și, prin urmare, gradientul este direcționat de-a lungul normalei la suprafața echipotențială în direcția creșterii potențialului energetic. Este evident că, în acest sens, modificările potențiale de energie mai rapid :. Astfel, putem concluziona că gradientul unei funcții scalare U este un vector direcționat perpendicular pe suprafață echipotențială U (x, y, z) = const în direcția creșterii funcției U. Lungimea sa este numeric egală cu derivata U normale la suprafețele echipotențiale . Această definiție este declarat a fi invariant. Nu este structurile depind de alegerea sistemului de coordonate.

Împreună cu suprafața echipotențială prin fiecare punct în spațiu poate deține o linie de putere așa-numitele. Direcția de tangentă la acesta, la fiecare punct în aceeași direcție ca și forța care acționează asupra unei particule în acest punct. Evident, liniile electrice și suprafețele echipotențiale sunt ortogonale reciproc între ele (fig. 4.8).

Folosind conceptul de gradient vto.poy legea lui Newton de mișcare într-un singur punct în câmpul de forță poate fi reprezentat ca.

Noi acum arată că din ecuația ar trebui să fie legea conservării energiei. Înmulțiți-l pentru partea dreaptă și partea stângă a ecuației în viteza scalar a particulei. .

Expresia din stânga poate fi rescrisă de derivata a energiei cinetice a particulelor, sau prin transferarea tot în partea stângă, și - obține legea de conservare a energiei. Rețineți că derivarea aici, era important ca energia potențială a particulei nu ar depinde în mod explicit de timpul t (de exemplu, cum). dependența de timp a fost o parte din energia potențială este doar în mod implicit. prin dependența de timp a particulelor raza vectorului (adică cum).