Ecuația universală a liniei fasciculului elastic

Luați în considerare Figura 5.1. Fasciculul de secțiune transversală constantă sub influența unei sarcini P extern este deformat, astfel încât punctul său final C este mutat în poziția C1. Axa neutră a fasciculului, denumit în continuare linia elastică, în punctul de coordonate z este 1 / r curbură. a deplasării y. unghiul q = ¢ y. al doilea derivat Ya.

Acești parametri sunt legate prin demonstrarea în geometria diferențială (5.1)

Pentru deplasări mici valori y „2 în comparație cu 1 poate fi neglijată, atunci: (5.2)

Luând în considerare (5.2) și (3.7.b), obținem:

Ținînd cont de relațiile (4.1) și (4.2), putem obține un lanț de relații diferențiale în cazul fasciculului cu secțiune transversală variabilă:

precum și un bar cu o secțiune transversală constantă:

În special, lemnul de încărcare, secțiune constantă, uniform distribuită q sarcină:

Prin urmare, diagramele în conformitate cu ecuațiile diferențiale (5.5), în funcție de parametrul luat în considerare, va avea următoarea formă (figura 5.2): q - linie orizontală, Q - panta linie dreaptă M - parabole pătratice, q - parabolică cubi, y - curba patrulea ordin. Dacă q = 0, dar este forța concentrată axa P. va fi îndoit de curba de ordinul trei. Dacă fasciculul este încărcat numai izkibayuschim momentul M. exprimat axa curbei de ordinul al doilea.

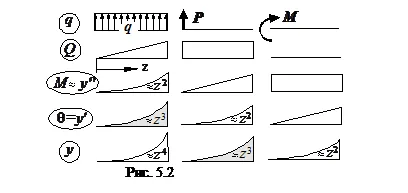
Cea mai mare alungire și tensiunea din tija se calculează prin formulele care rezultă din (4.6) și (4.7):

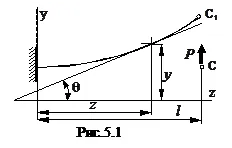
Definiți deformarea grinzii, prezentată în figura 5.1. Momentul de încovoiere la secțiunea z este egal cu: M = P (l - z)

După dubla integrare de exprimare

Integrarii constanta C 1 se constată din condiția la limită: dacă z = 0imeem: ¢ y = 0. Prin urmare C1 = 0, dar pentru soluții generalitate încă părăsi acest termen în formula:

Integrarii constanta C 2 se determină din condiția la limită: z = 0 când y = 0. Prin urmare, C2 = 0, atunci pentru un punct arbitrar:

Unghiul maxim de înclinare și deformarea are loc în punctul de aplicare al forței F.

Astfel, pentru z = l avem:

Ecuația universală a liniei fasciculului elastic

Din Exemplul 5.1 arată că există două constante arbitrare (C1, C2 5.9) pentru fiecare porțiune de grindă după integrarea ecuației. Dacă fasciculul are n site-uri, pentru a determina integrarea 2n constante trebuie să lucreze împreună pentru a rezolva ecuații 2n. Pentru a transmite o rigiditate constantă EJx acest lucru poate fi evitat în pregătirea liniei elastice a ecuației să urmeze anumite reguli.

Să considerăm fasciculul (figura 5.3), încărcat cu cele mai comune tipuri de tensiuni: momentul concentrat Ma. punct forță P și intensitate distribuită q sarcină. Dintre aceste tipuri de factori de putere pot fi combinate cu aproape toate care apar în practică, tipuri de sarcini. Pentru direcțiile pozitive ale forțelor care se deplasează de la capătul din stânga va lua cele indicate în figură, și anume P și q - în sus, și pentru o clipă Ma - sensul acelor de ceasornic. specificat sistem de factorul de putere trebuie să îndeplinească condițiile de echilibru.

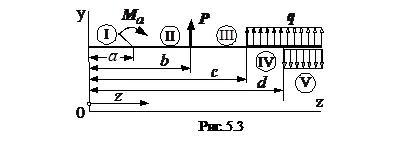
Reveal caracteristici introduse în ecuația de linie elastic diferitele tipuri de forțe externe. Pentru a face acest lucru, fac o expresie momentelor de încovoiere pentru fiecare dintre cele cinci domenii menționate mai jos:

Se vede că momentul de încovoiere pentru fiecare secțiune ulterioară implică în întregime expresia momentului de încovoiere a secțiunii anterioare și este diferită de adăugarea termenului nou. În tranziția de la a patra porțiune menționată a cincea model special stocat. Astfel, o sarcină distribuită uniform a secțiunii a patra a continuat, așa cum se arată în fantomă, în a cincea porțiune și cea de-a cincea porțiune aplicată simultan negativă (compensarea) intensitatea q sarcinii.

Noi integra expresia rezultată o dată, fără a dezvălui paranteze. Pentru a menține uniformitatea expresiilor obținute, integralei unei write Vi Vi (z-a), care va afecta numai magnitudinea unei Ci constante arbitrare. Ca urmare, ținând cont de expresia = M Ya / EJx obține următoarea expresie pentru linia de elastic unghiul y „:

Constantele Arbitrar Ci. Acestea ar trebui să fie alese astfel încât trecerea de la o secțiune la alta valoare y „nu a suferit ruptura. Prin urmare, cu z = și u'1 = y2, dacă j2 z = b = u'3, și așa mai departe.

Deoarece fasciculul are o rigiditate constantă, este evident că

Q0 Linia elastică unghiul de înclinare la origine se determină din expresia pentru prima secțiune:

Integrarea expresiile obținute pentru a doua oară, se va găsi:

Constantele Arbitrar Di. Acesta trebuie să fie ales din starea de continuitate a funcției y la frontieră. Prin urmare, cu z = și y1 = y2, dacă z = b = y2 y3 etc. Deoarece fasciculul are o rigiditate constantă, este evident că

,

în cazul în care y0 - și coordoneze linia elastică la origine. Ecuația (5.14) este convenabil scrisă sub forma așa-numita linie de grindă comună, elastică a ecuației universale. (5.15)

Pentru a determina coordonatele punctelor ale liniei elastice a primei porțiuni trebuie utilizată de către membrii ecuației la stânga liniei verticale cu index I. Pentru a doua porțiune necesară pentru a prelua termenii cu caracteristici index II. etc. Pentru a determina ordonata la a cincea stația ar trebui să efectueze calcule, folosind ecuația completă 5,15. Avantajul ecuației universale este că vă permite să facă ecuația liniei elastice, ocolind definiția greoaie de constante arbitrare. Indiferent de numărul de site-uri, este necesar să se determine numai două constante: V0 și Q0.

Scrieți ecuația liniei elastice la consola cu capătul din stânga rigid prinse și încărcate într-o porțiune de mijloc a q sarcină distribuită (Figura 5.4). Se determină reacția și momentul în sigilarea:

Acum este posibil, în locul sigiliului stâng în schema echivalentă trage susține reacția. Astfel, schema de redus la forma pentru care este scris în ecuația universală. Originea este pus la capătul din stânga al fasciculului. Aici Q0 = 0 și y0 = 0.

Mai departe, din ecuația (5.15) „recruta“ din ecuație termenii corespunzătoare razei luate în considerare.

Prima porțiune include forța de termeni și cuplul în zadelke. În cea de a doua porțiune este adăugată pentru a le sarcina pe termen distribuit. Cea de a treia porțiune a deplasării definită toți termenii ecuației. Dacă deschideți paranteze, apoi ultima secțiune obținem:

.

Aici, linia elastică este o linie dreaptă, din momentul de îndoire este zero.