ecuația Laplace și funcțiile armonice

Vom începe cu cele mai simple și ecuațiile de mai-eliptic, care anume ecuația Laplace. Această ecuație ecuație are forma

Aici, f (x) - o anumită funcție. Dacă f (x) ≠ 0. apoi setați-ecuația (1) este ecuația neomogenă Laplace. Dacă f (x) = 0 avem ecuația Laplace omogenă

ecuația Laplace neomogene este adesea numită ecuația Poisson.

Într-o înregistrare mai detaliată a ecuației Laplace - neomogena-nativ și uniform - sunt după cum urmează:

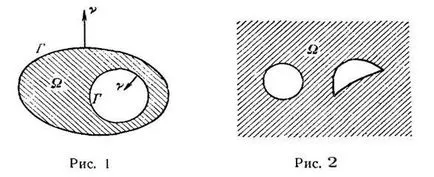
Luați în considerare o suprafață închisă F nu este conectat în mod necesar „și lăsați-F limitează domeniul de aplicare al # 8486;, final (fig. 1) sau infinit (Figura 2) In ambele cu LES-ceaiuri presupune „că suprafața în sine D este finit. Ecuația comportamentului Budemizuchat omogen Laplace în aceste zone.

U (x) este numit armonica într-o regiune finită # 8486;, dacă este în această zonă este de două ori continuu diferențiabilă și satisface ecuația Laplace omogenă.

Noi spunem că funcția u (x) armonic în câmpul infinit-finit # 8486;, în cazul în care în fiecare punct al acestei regiuni, situată la capătul sau începutul regiunii, u (x) este de două ori continuu diferențiabilă, udovletvoryayi ecuație Laplace omogenă la infinit și este de ordinul

,astfel încât suficient de mare pentru | x | inegalitate

unde m - dimensiunea spațială și C - este o parte constantă evaluate. În cazul regiunii bidimensional (m = 2) Condiția (3) înseamnă că-chaet armonic în domeniu infinit este mărginită la infinit.

Subliniem că determinarea unei funcții armonice otno-sitsya numai în cazul zonei deschise (de exemplu, multitudinea de deschise conectate ..); Dacă vorbim despre armonica funcții într-o zonă închisă, prin aceasta ne referim că funcția este armonic într-un câmp larg deschis.

De asemenea, observăm că definiția unei funcții armonice nu impune restricții asupra comportamentului funcției pe granița.

Exemplul 1: Dacă # 8486; - regiunea infinit, funcția u (x) = 1 armonic numai dacă m = 2. Dacă m> 2. în regiunea infinită, această funcție nearmonic. Cu toate acestea, guar monichna în orice domeniu finit, pentru orice t.

Exemplul 2. Într-o funcție plan bidimensional

unde z = x + IV. armonic în orice zonă care nu conține originea.

Exemplul 3. Funcția

z = x + iy. armonic în cercul | z |

Exemplul 4: O funcție de două variabile u = x 2 + y 2 nu este un Xia armonic în orice domeniu, deoarece acesta nu satisface ecuația Laplace-ryaet omogen

Exemplul 5 Funcția u = x2-y2 armonic în orice zonă finită clorhidric.

În planul bidimensional al unei transformări conformal nu modifică ecuația Laplace omogenă. În cazul în care orice astfel că nu este așa, dar încă mai există o transformare care Perevi-dit orice funcție armonică în aceeași armonica. Această transformare Kelvin, care ia punctul

x (xl, x2. xm) la x „(h'i x'2. x'm). simetric în raport cu un punct x al sferei de raza R centrată la originea și funcția clorhidric dată și (x), în funcție

Să ne amintim că punctele X și X „sunt numite simetric în raport cu zonele enumerate mai sus, dacă acestea se află pe aceeași rază care emană de la origine, și în cazul în care | x | • | x „| = R2. Coordonate carteziene-ordonate puncte simetrice sunt legate de

, Deși destul de greoaie de calcul simplu conduce la relația