Ecuația d
Ecuația lui Bernoulli
Ecuația Daniila Bernulli este ecuația de bază a hidrodinamică. Sub această ecuație versat pentru echilibru lin varierea mișcare fluidă sunt rezolvate prin care problemele de bază ale hidrodinamicii. Noi introducem conceptul de energia specifică a fluxurilor elementare și curentul de lichid.

fluid în masă ocupă un anumit volum V, care se află sub presiune egală cu energia de presiune r.Potentsialnaya rV.Udelnaya aceeași potentsialnayaenergiya presiune energiipV egală cu potențialul împărțit de către forța tyazhestidannogo obemagV, t. e.
aprovizionare completă a masei specifice a energiei fluidului este egală cu suma lor, r. F., și având în vedere expresiile (a) și (b), putem scrie
Mai mult, masa lichidului m se deplasează cu o viteză și are o energie cinetică; dar gravitatea acestei mase este egală cu mg, iar energia cinetică specifică a jeturilor egal
Adăugarea de expresie (c) și (g), obținem o expresie complete fluxuri elementare udelnoyenergii
Aici - energia cinetică specifică;
- energie de presiune specifică și poziția.
Fluxul de energie specifică suma totală E izudelnoy a potențialului de energie și energia cinetică specifică Ekpotoka.
Pentru cazul schimbării lin constantă de curgere a fluidului de energie potențială specifică în toate punctele secțiunii transversale efective este același și egal la
Curgerea fluidului este considerat ca fiind un set de n fluxuri elementare, fiecare dintre care are energia cinetică specifică. Această valoare este diferită pentru diferite fluxuri care formează flux.
Definim valoarea medie a acestei cantități în secțiunea de curgere. Pentru a face acest lucru, viteza reală a U1 fluxuri elementare. u2. ONU înlocui medie a vitezei de curgere v; atunci valoarea medie a energiei cinetice specifică a fluxului în această secțiune este egală cu
Aici, un - coeficient de Coriolis care reflectă neuniformitatea distribuției vitezei pe secțiunea transversală a fluxului (ajustarea sau energia cinetică).
Un factor adimensional este raportul dintre energia cinetică a fluxului real la energia cinetică calculată din viteza medie. Dacă profilul de viteză în secțiunea transversală de curgere este aproape dreptunghiulară, adică Viteza la diferite puncte apropiate de media, apoi un coeficient de Coriolis aproape de unitate. În cazul în care viteza în secțiunea transversală diferă în mod semnificativ unele de altele, iar apoi un coeficient este mult mai mare decât unitatea.
Să considerăm, de exemplu, adâncimea de curgere h = 6 m, în secțiunea transversală a căror viteze sunt distribuite pe triunghiul, adică în partea de jos a vitezei este zero și se ridică la suprafață conform legii să direcționeze cea mai mare valoare ipov = 3 m / sec. Medie viteza v = 1,5 m / s, iar energia cinetică corespunzătoare
Estimăm energia cinetică a fluxului de precizie. Pentru aceasta, vom lua trei puncte de la o înălțime h1 = 1m; h2 = 3 m și h3 = 5m, care se află în straturile de mijloc de înălțime egală de 2 m fiecare. Viteza la aceste puncte, respectiv u1 = 0,5; u2 u3 = 1,5 și = 2,5 m / sec. Energia cinetică a acestor trei viteze
care este mai mare decât rata medie.
Coeficientul de Coriolis obținut
.
Bazat pe prelucrarea a numeroase date colectate în râuri și canale, se constată că pentru fluxuri mari deschise. În mișcare uniformă în conducte și canale practic.
În viitor, cu excepția cazului în care prevede în mod expres altfel, se iau pentru a simplifica calculele. Cu toate acestea, trebuie amintit că, în unele cazuri, distribuția neuniformă a vitezei poate fi o valoare semnificativ mai mare decât 1 (două sau mai multe).

Adăugarea de energie potențială cinetică specifică și specifică a fluxului, obținem formula energia specifică totală a fluxului
,
și ținând cont de expresia (e) și (g), avem
, (72)
și anume densitatea totală a fluxului de energie specifică egală cu suma specifică cinetică și potențială (presiune și poziție) fluxul de energie. Să ne amintim că toate constatările făcute pentru echilibru, schimbând gradat mișcarea lichidului.
Ecuația lui Bernoulli pentru fluxuri elementare. Selectați în flux constant reală a trickle elementar lichid (Fig. 21) și să definească energia specifică a lichidului în două secțiuni arbitrare 1-1 și 2-2. poziții de înălțime ale centrelor de prima și a doua secțiuni sunt, respectiv și z2 z1; presiune hidrodinamice și aceleași puncte p1 și fluxul p2 rata - u1 și u2. Apoi, densitatea de energie totală a fluxurilor elementare în secțiunea 1-1, pe baza formulei (71) este egal cu
Aproape întotdeauna, din moment ce o parte din cantitatea totală de energie cheltuită în depășirea forței de rezistență (frecare) atunci când lichidul se deplasează de la secțiunea 1-1 la secțiunea 2-2. Notăm aceste pierderi. Apoi, în conformitate cu legea de conservare a energiei se poate scrie că, și având în vedere expresiile (g) și (h), obținem
. (73)
Ecuația (73) și are o ecuație Bernoulli pentru fluxurile elementare ale unui fluid real, în timpul mișcării de echilibru, care stabilește legătura între viteza de deplasare, presiunea în fluid și poziția unui punct în spațiu. Este valabil pentru oricare două secțiuni astfel încât secțiunile 1-1 și 2-2 au fost luate în mod arbitrar. Ecuația (73) și pot fi reprezentate grafic (fig. 21). Dacă vom combina nivelele de lichid în piezometre atașate la mai multe secțiuni, obținem o p-p-line, care se numește linia piezometrică și arată variația energiei potențiale specifice de-a lungul lungimii fluxurilor elementare. Dacă vom conecta punctele care, în fiecare secțiune transversală verticală descriu energia totală specifică (și astfel de termeni pot primi, într-adevăr, ca cm. Mai jos), obținem o linie N-N. Se numește napornoyliniey sau o linie de putere; se arată schimbarea în densitatea totală de energie de-a lungul lungimii de fluxuri. Apoi, distanța verticală dintre secțiunea transversală în orice plan orizontal I -I. care corespunde stocului inițial de energie specific în prima secțiune, iar linia de presiune N-N dă valoarea pierderilor de energie hw pentru a depăși forțele de rezistență la secțiunea din prima secțiune a acestei secțiuni, iar distanța dintre presiunea și liniile piezometrice - energia cinetică specifică într-o anumită secțiune u2 / 2g.
Pentru un lichid ideală, în care nici o forță de frecare în ecuația (IV.7) hw = 0 și ecuația Bernoulli devine
Dar, așa cum secțiunea 1-1 și 2-2 sunt luate la întâmplare, în forma generală a ecuației lui Bernoulli la fluxurile elementare ale unui fluid perfect este scris după cum urmează:
Ecuația debitului Bernoulli. Luați în considerare la flux constant, lin schimbarea mișcării (Fig. 22). Am ales în mod arbitrar două secțiuni 1-1 și 2-2. axele pe care, respectiv, au și z2 z1 - verticală de coordonate axa curentului deasupra unui plan arbitrar o comparație-o, p1 și presiune hidrodinamică p2 în aceleași puncte V1 și V2 - viteza medie în secțiunile 1-1 și 2-2.
Debitul specific de energie totală determinată prin formula (72): secțiunea transversală 1-1
,
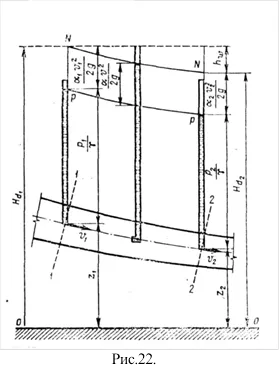
Evident, din moment ce o parte din energia care urmează să fie cheltuite învingând forța de rezistență (frecare). Notăm o pierdere de energie în acest domeniu -. Apoi, putem scrie că și, înlocuind valorile, obținem
Ecuația (74) se numește ecuația Bernoulli pentru ecuația principală și potokazhidkosti hidrodinamica; Am obținut cu ea multe formule și de a rezolva o serie de probleme practice. Ecuația Bernoulli stabilește o relație matematică între elementele principale ale mișcării fluidului, adică. E. Viteza medie și presiunea hidrodinamică.