Econometrie (9) - Tutorial, pagina 3
14. Estimarea Folosind un model de regresie. Punct și previziuni interval
Predicția este obținută prin substituirea în ecuația de regresie Y = a0 + a1x.
Aici A0, A1 - parametrii care sunt estimate din datele statistice. Ele se numesc coeficienții de regresie.
În cazul Y la efectul conjugat al mai multor factori (x1, x2. Xn) ecuația devine
Y = a0 + a1x1 +. + Anxn.
În primul caz avem R. perechea a doua - la plural) variabile. Rezultatul este o estimare a valorii medii a variabilei dependente la aceste niveluri factorul de argumente. Pentru ecuația de regresie este determinată de obicei intervale de încredere, care pot fi, de asemenea, utilizate în prognoză.
Prognoza punctul - o previziune care indică o valoare unică cifra proiectată. Valoarea specifică.
15. Încălcarea condițiilor homoskedasticity: heteroscedasticitate, autocorelație
Heteroscedasticitatea și autocorelație acestei încălcări a condițiilor homoscedasticity (a doua și a treia condiție Gauss-Markov). De obicei, luate în considerare două opțiuni condiții încălcare homoscedasticity:
1. Erori au varianța diferite pentru diferitele observații - Heteroscedasticitatea. Heteroscedasticitatea - „răspândirea inegală a“ distribuției teoretice de membru aleatoriu este diferit pentru diferitele observații din eșantion
De exemplu, dacă luăm în considerare dependența de restul costurilor salariale, este logic să se presupună că răspândirea va fi mai mare pentru persoanele mai bogate.
2. Erorile au varianță constantă, dar neyavlyayutsya independent Acest fenomen se numește autocorelație
Cazul general al unei transformări simplu pentru a realiza homoscedasticity In general:
1. Se calculează mai mici pătrate estimări ale coeficienților de regresie
2. Găsiți EI reziduuri și pătrate EI2
3. Găsiți logaritmii remanențelor pătrat ln (EI2)
4. Se calculează regresia ln (EI2)
5. O ln predicție (EI2) prog
6. Găsiți wi greutăți = observații exp (ln (EI2) prog)
7. Greutatea wi a primit este utilizat într-o metodă a celor mai mici pătrate ponderate
Consecințele heteroschedasticitate și autocorelatie conduce la coeficienții de regresie ineficienta rezultat (dar acestea rămân imparțial) și la un calcul eronat al t observate și F-statistici.
16. Metoda celor mai mici pătrate generalizată, Aitken teorema
Utilizarea celor mai mici pătrate cu încălcarea condițiilor homoscedasticity conduce la următoarele consecințe negative:
1. estimând coeficienții de necunoscuți β sunt ineficiente, adică există alte estimări care sunt imparțiale și au o dispersie mai mică.
2. Erorile standard ale coeficienților de regresie sunt subestimate și, în consecință, t -Statistics - umflate, și va fi primit o idee greșită a preciziei ecuației de regresie.
Generalizat metoda celor mai mici pătrate
Considerăm metoda de estimare, atunci când starea homoscedasticity, matricea este β = (Ω-1 XT X) -1 HT Ω-1y
Calculul coeficienților de regresie necunoscute ale acestei ecuații sunt numite generalizate mai mici pătrate (OLS).
Aitken Teorema: în încălcarea estimărilor ipotezelor homoscedasticity obținute metoda celor mai mici pătrate generalizată, sunt imparțiale și cea mai eficientă (având cea mai mică variație). În practică, uj matrice este aproape niciodată cunoscut. Deci, de multe ori să încerce orice metodă de evaluare a matricei de evaluare uj și să le utilizeze pentru evaluare. Această metodă se numește metoda patratelor accesibil generalizată.
17. Teste pentru heteroschedasticitate: Spearman, Breusch-pagani, alb, Goldfeld-Quandt
corelație Rank. testul de corelație rang Spearman
Locul de observație a variabilei - numărul de variabile de observare într-o secvență crescătoare ordonată.
Testul Spearman rank test de corelație pentru heteroscedasticitate, stabilind că deviația standard a elementului rezidual de regresie are o relație non-liniară strictă cu variabila explicativă.
În cazul în care testul de rang de corelație Spearman se presupune că elementul de dispersie întâmplare va crește sau descrește odată cu creșterea x, și, prin urmare, în regresie, evaluată de OLS, valorile absolute ale reziduurilor și valorile lui x sunt necorelate. Datele privind x si soldurile sunt ordonate. Presupunând că coeficientul de corelație generală corespunzătoare a populației este zero, adică Heteroskedasticity absent, coeficientul de corelație rang are o distribuție normală cu media 0 și varianța 1 / (n - 1) în eșantioane mari.
Cele mai populare criteriul formal este un criteriu propus de R. S. Quandt și Goldfeld.
În timpul încercării în conformitate cu acest criteriu presupune că deviația standard a distribuției de probabilitate u proporțională cu valoarea lui x în această observație.
Se presupune, de asemenea, că termenul aleator este în mod normal distribuită și nu este supusă de autocorelare.
Cu alte cuvinte de test Goldfelda- Quandt - test pentru heteroscedasticitate, stabilind că abaterea standard a regresie crește pe termen reziduale atunci când variabila explicativă în creștere.
Toate observațiile n din eșantion sunt sortate în funcție de mărime x, după care regresia individuală estimată pentru prima n „și pentru ultimele n“ observații;
Medie (2n n- „) sunt eliminate observații.
Dacă ipoteza cu privire la natura heteroscedasticitate este adevărat, iar variația în ultimele n „observații va fi mai mare decât în primul n“. iar acest lucru se va reflecta în suma pătratelor reziduurilor din cele două regresii „private“.
Notăm suma pătratelor reziduurilor în regresii pentru prima n „iar ultima n“ observațiile, respectiv, prin RSS1, și RSS2,
Calculăm raportul RSS2 / RSS1, care are o distribuție cu F (n „- k - 1) și (n“ - k - 1) grade de libertate, în cazul în care k este numărul de variabile explicative în ecuația de regresie.
Metoda Goldfeld-Quandt poate fi de asemenea utilizat pentru a testa Heteroskedasticity presupunând că σ. este invers proporțională cu x.
Utilizați aceeași procedură ca cea descrisă mai sus, dar acum RSS1 testul statistic index / RSS2, care are din nou un F-distribuție cu (k n'- - 1) și (n „- k -1) grade de libertate.
Notăm suma pătratelor reziduurilor în regresii pentru prima n „iar ultima n“ observațiile, respectiv, prin RSS1, și RSS2,
Calculăm raportul RSS2 / RSS1, care are o distribuție cu F (n „- k - 1) și (n“ - k - 1) grade de libertate, în cazul în care k este numărul de variabile explicative în ecuația de regresie
Astfel, testul Goldfeld-Quandt constă din trei etape:
toate observațiile din eșantion sunt sortate în ascendent x.
luate primele și ultimele n observații (o treime din toate), evaluate două regresii diferite și sunt RSS1 și RSS2
Pentru relația RSS2 / RSS1, efectuat testul Fisher (n '- k - 1) și superioară (n' - k - 1) mai mic de grade de libertate, unde k - numărul de variabile explicative în regresie.
Testul este aplicabil în ipoteza că varianța depinde de unele variabile suplimentare:
1. Construiți ecuația de regresie, iar resturile sunt calculate:
2. Se calculează estimarea reziduurilor varianța:
3. Construiți ecuația de regresie auxiliară
4. Pentru ecuațiile de regresie auxiliare definesc variația explicată a RSS.
5. Găsiți statistica de încercare:
6. În cazul în care ipoteza H0: resturile de homoscedasticity că BP are o statistica de distribuție. Ie prezența heteroscedasticitate reziduurilor la nivelul de semnificație arată:
Când Heteroskedasticity poate fi ajustat:
Se presupune că varianța asociat cu variabilele explicative în forma:
pentru că dispersii nu sunt cunoscute, ele sunt înlocuite cu pătrate estimează abateri EI2.
Algoritmul aplicație (de exemplu, trei variabile)
1. Construiți ecuația de regresie, iar resturile sunt calculate.
2. Evaluarea ecuația de regresie auxiliară:
3. Se determină ecuația statistica testului auxiliar
4. Verificați semnificația generală a ecuației prin utilizarea 2 criteriu.
test de alb este mai generală decât testul Goldfeld-Quandt.
Dezavantajul utilizării testului White: Dacă respinge ipoteza nulă a homoscedasticity nu este clar ce să facă în continuare.
18. Corectarea heteroscedasticității: logaritmi, regresie ponderată, cazul general
De multe ori prezența heteroscedasticitate în regresie indică reziduurile nepravelnoy caietul de sarcini model.
Luați în considerare două modele - liniare
yi = SS0 + ß1xi + εi
Modelul liniar al unui membru prisudstvuet aleator aditivă formă și într-un model logaritmic - multiplicativ.
Formularul multiplicativ reflectă influența puternică a termenului perturbare pentru valori mari ale covariabilele și mai slabe - pentru cei mici.
Prin urmare, în cazul în care modelul liniar există acest tip de heteroscedasticitate, este foarte posibil ca în modelul logaritmică nu este heteroscedasticității.
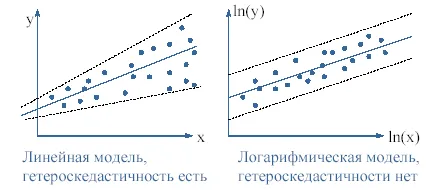
regresie logaritmică nu este întotdeauna posibil pentru a scăpa de heteroscedasticitate. În plus, modelul logaritmic nu satisface întotdeauna obiectivele studiului (necesar pentru a estima dependența de Veličná absolută în loc de elasticitate)
În aceste cazuri, o altă abordare - o regresie ponderată.
yi = SS0 + ß1xi + εi
Să Modelul presudstvuet heteroschedasticitate
Și noi știm valoarea exactă a variației σi2 modelului de eroare
(Urmat de formule și soluții, nu cred că trebuie să picteze, așa că nu va bloca mințile voastre luminoase, cu tot felul de soluții)
La urma urmei a fost calculat. astfel, membru model aleator are o dispersie constantă (calculată este egală cu 1) și, prin urmare, OLS convenționale necunoscute koefitsent să fie imparțiale și eficiente.
În practică, variația de eroare este aproape niciodată. Dar, uneori, se poate presupune că σi2 este proporțională cu o zi variabilă.
Apoi, ponderile observațiilor trebuie să utilizeze valoarea 1 / zi:
Varianța unui membru aleatoriu a unui astfel de model este, de asemenea, constantă
Destul de des, ca o variabilă, interconectată cu o variație a unui membru oarecare al regresor poate fi utilizat:
În acest caz, modelul ponderat este după cum urmează:
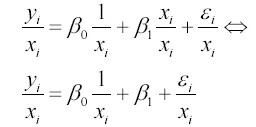
SS1 Koefitsent în modelul transformat corespunde unui membru gratuit.