Dualitatea în programarea liniară

definiții de bază ale teoriei dualității.

Fiecare problemă de programare liniară poate fi asociată cu o altă problemă de programare liniară. În rezolvarea uneia dintre ele va fi rezolvată în mod automat o altă problemă. Astfel de probleme sunt numite vzaimodvoystvennymi. Ne arată cum la această problemă (vom numi originalul) pentru a construi dubla sale.

Luați în considerare problema producției planificate.

Conținutul formulării problemei directe. un astfel de plan, de ieșire X = (x1, x2. xn), în care profitul (venituri) din vânzarea produselor este maxim, cu condiția ca consumul de resurse al fiecărui produs trebuie să depășească rezervele disponibile.

Reguli generale pentru întocmirea problema dublă.

Funcția obiectiv (min)

Partea dreaptă a limitărilor

Funcția obiectiv (max)

A - matrice constrângere

A T - matrice constrângere

i-lea constrângere: ≥ 0, (≤ 0)

Variabila yi ≥ 0, (≤ 0)

Constrângerea i-lea: 0 =

Variabila yi ≠ 0

Variabila xj ≥ 0

J-constrângere: ≤ 0

Variabila xj ≠ 0

j-lea constrângere: 0 =

Noi construim sarcina sa dublă de după reguli.

Numărul de variabile în problema duală este numărul de inegalități în original.
Matricea Coeficientul problemei dublă este transpusă la coeficienții matricei originale.
Coloana de termeni liberi de problema originală este un șir de coeficienți pentru funcția obiectiv a dublu. Funcția obiectiv este maximizată într-o sarcina la alta este redusă la minimum.
Condițiile de non-negativitate variabilelor corespund problemei inițiale, constrângerile duale ale inegalității vizează alt mod. Pe de altă parte, inegalitățile, restricțiile în original, la o concordanță condițiile de nenegativitate duală.

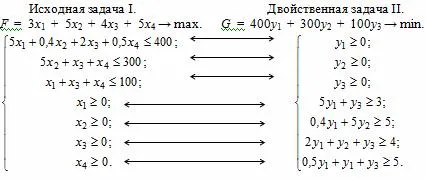
Rețineți că sarcina I rânduri de coloane ale matricei sunt probleme II. Prin urmare, coeficienții variabilelor în problema yi II - sunt, respectiv, coeficienții de i-lea problema inegalității I.
Modelul rezultat este modelul economic și matematic al problemei duală a problemei directe.

Pentru a construi problema duală folosind acest serviciu

Inegalitățile sunt conectate prin săgeți, sunt conjugate.
producție substanțială a problemei dublă. găsi un preț stabilit (estimativ) resurse Y = (y1. y2. um), în care costul total al resurselor vor fi minime, cu condiția ca costul resurselor în producția fiecărui produs nu va fi mai mică decât profitul (venituri) din vânzarea acestor produse.
prețurile de resurse y1. v2. um în literatura economică le-am primit diverse nume: de înregistrare, implicit, umbra. Semnificația acestor nume este că este condiționată, prețurile „nu reale“. Spre deosebire de prețurile „externe“ c1. s2. cn produs cunoscut, de regulă, înainte de începerea producției de resurse prețurilor Y1. v2. um sunt interne, deoarece acestea sunt setate nu este din exterior, dar sunt determinate în mod direct, ca urmare a rezolvării problemei, astfel încât acestea sunt adesea numite estimările de resurse.
Comunicare primar și probleme duale este, în special, că soluția la una dintre acestea pot fi obținute direct de la alte soluții.

teoreme de dualitate

Dualitatea este un concept fundamental în teoria programării liniare. Principalele rezultate ale teoriei dualității închise în două teoreme, numite teoreme de dualitate.

În prima teorema de dualitate.

Dacă unul dintre o pereche de probleme duale I și II este rezolvabilă, este rezolvabilă și celălalt, cu funcția obiectiv în planurile optime coincid, F (x *) = G (y *), unde x * y * - soluții optime I și II

A doua teoremă de dualitate.

Planuri x * și y * sunt optime în probleme I și II, dacă și numai dacă pentru înlocuirea lor în sarcini de restricție I și II, respectiv, cel puțin unul din fiecare pereche de inegalități conjugate devine o egalitate.
Aceasta este teorema de bază dualitate. Cu alte cuvinte, în cazul în care x și y * * - soluții acceptabile probleme primare și duale și dacă c T x * = b T y *, atunci x * și y * - soluții optime cu dublă pereche.

Teorema a treia dualitate. Valorile variabilelor yi în soluția optimă a problemei duale se evaluează impactul termenilor liberi constrângerile de sistem bi - inegalitățile problemă directă privind valoarea funcției obiective a acestei probleme:
δf (x) = yi bi

Rezolvarea metoda ZLP simplex, vom rezolva simultan dual ZLP. Valorile variabilelor problemei yi dublă. în planul optim numit determinat în mod obiectiv, sau estimări duble. În probleme aplicate estimări duale Yi numit de multe ori, prețurile ascunse umbră sau estimări ale resurselor marginale.

Proprietatea este reciproc probleme duale

Problema unul în căutarea pentru un maxim de o funcție liniară, celălalt - cel puțin.
Coeficienții variabilelor într-o funcție liniară a unei singure sarcini sunt membri fără restricții ale sistemului la altul.
Fiecare dintre sarcinile definite într-un format standard, în care se pune problema de a maximiza tuturor inegalităților formează ≤. și problema reducerii la minimum toate tipurile de inegalitate ≥.
matricea coeficienților la variabile în limitele ambelor sisteme sarcini sunt transpuse reciproc:
Numărul inegalităților în limitările de sistem ale unei probleme coincide cu numărul variabilelor într-o sarcină diferită.
Condițiile de non-negativitate a variabilelor disponibile in ambele probleme.

Deci, avem problema originală I și soluția optimă x * = (0, 40, 0, 100) și F (x) = 700.

Aplicând teorema de dualitate, vom obține soluția problemei duală a soluției cunoscută a problemei inițiale.
Vom găsi o soluție la problema duală a II y * = (Y1. Y2. Y3), fără a recurge la metoda simplex, și folosind cea de a doua teorema de dualitate și cunoscut planul x * optim.

Luați în considerare inegalitățile problemă I prin substituirea x * în constrângerile de sistem.

Constrângerea este îndeplinită ca o inegalitate strictă, și anume nu este atins de resurse de primul tip. Deci, acest lucru nu este o resursă limitată și evaluarea sa în planul optim y1 = 0.

* 40 + 5 0 + 100 = 300 = 300

constrângere problemă directă este îndeplinită ca o egalitate. Aceasta înseamnă că 2 minute resursă este utilizată în întregime planul optim este rară și evaluarea acestuia în conformitate cu teorema nenul doua dualitate (y2 ≠ 0)

0 + 0 + 100 = 100 = 100

A patra constrângere în problema duală este egalitate
0,5y1 + y2 + y3 = 5

De la 1, 5, 7 inegalități stricte (au semnul "<" или ">. „), Atunci inegalitatea corespunzătoare Problema II a unei perechi de conjugat necesar să se aplice egalitatea avem:

și anume y * = (0, 1, 4) - soluția optimă.

Astfel, în virtutea celei de a doua teorema de dualitate, am găsit rapid soluția optimă Obiectivul II, care profitând de condiția că egalitatea este cel puțin una dintr-o pereche de disparități conjugate în restricții de probleme duale.

Între variabilele problemei inițiale și variabilele duale, există o legătură profundă. Și anume, după aducerea celor două probleme I și II la forma canonică a variabilelor primare și secundare ale problemei corespund reciproc, după cum urmează:

După ce a stabilit această relație, se poate observa că prin rezolvarea problemei simplex I și primit de către ultimul tabel simplex (Tabel.), De fapt, ne rezolva problema și II.

Scriem masa, ținând cont de corelația dintre variabilele x i și YJ.

În virtutea corespondenței și II ale y1 variabile dualitate teorema. v5. U7 li se cere să fie egal cu 0, deoarece x5. x2. x4> 0 strict. 4. O variabila y y 2 y 3 y 6. ia valori de la linia de index 1, 1, 1, 4, respectiv, variabilele lor x1 corespunzătoare. x6. x3. x7 = 0, liber. Deci, din acest din urmă problema din tabelul II, fără a face calcule, și chiar folosind doar variabilele corespunzătoare:

Reguli de introducere a datelor

Puneți întrebări sau să facă sugestii sau comentarii pot fi partea de jos a paginii, în secțiunea Disqus.
Puteți trimite, de asemenea, o cerere de ajutor în a face cu examene de partenerii noștri de încredere (aici sau aici).