Distribuția variabilei aleatoare discrete

Într-un note anterioare, care indică faptul că rezultatul testului poate fi o variabilă numerică. La rândul său, variabilele numerice sunt împărțite în discret și continuu. Variabilele discrete caracteristice pentru transferuri și numărare și continue - pentru măsurare. In aceasta și în următoarele câteva articole vor examina situația generală și distribuția cea mai răspândită, care descrie o variabilă aleatoare discretă. [1]

Distribuția variabilă aleatoare discretă - aceasta este o listă exhaustivă a tuturor valorilor posibile ale unei variabile aleatoare, în cazul în care fiecare rezultat este furnizat în conformitate cu probabilitatea. De exemplu, în Fig. 1 prezintă distribuția numărului de credite ipotecare emise în termen de o săptămână filiala locală a băncii. După cum arată tabelul de toate posibilele rezultate, suma probabilităților lor este 1.

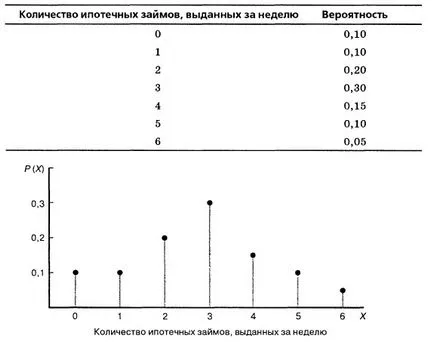
Fig. 1. Distribuția numărului de credite ipotecare emise într-o săptămână

Așteptări μ velichinyX aleatoare discret numit valoarea medie a distribuției sale. Această valoare este suma produselor tuturor valorilor variabila aleatoare X la probabilitatea corespunzătoare P (X). Cu alte cuvinte, speranța unei variabile aleatoare discrete X - este o medie ponderată a tuturor rezultatelor posibile, în cazul în care greutățile sunt probabilitățile fiecărui rezultat.

în care Xi - i -e valoare discretă a variabilei aleatoare X. F (Xi) - i -Ro valorile de probabilitate ale unei variabile aleatoare discrete X.

Numărul estimat de credite ipotecare emise în această săptămână:
p = 0x0,01 + 1 x 0,1 + 2 x 0,2 + 3 x 0,3 + 3 x 0,15 + 5 x 0,1 + 6 x = 0 + 0,05 0,1 + 0, + 0,9 + 4 0,6 + 0,5 + 0,3 = 2,8

Notă: numărul estimat de credite ipotecare emise în această săptămână, exprimate de un număr, care nu are un sens literal, deoarece numărul de credite poate fi măsurat numai cu numere întregi.

Dispersiyaσ două discrete variabila aleatoare X este o medie ponderată a diferențelor pătrate între toate valorile posibile și așteptări. Greutățile sunt probabilitățile rezultatelor corespunzătoare:

în care Xi - i -e valoare discretă a variabilei aleatoare X. F (Xi) - i valorile de probabilitate ale -lea un X. variabile aleatoare discrete

Abaterea standard sigma a unei variabile aleatoare discrete:

În Excel pentru a calcula statistici descriptive discrete variabile aleatoare au funcții standard, cu toate acestea, sunt utilizate în general coloane pur și simplu suplimentare pentru calculele intermediare în conformitate cu formulele (1), (2) și (3), a se vedea. Fig. 2. Singura excepție - așteptarea - este posibil să se determine imediat (calcule intermediare) folosind = SUMPRODUCT ().

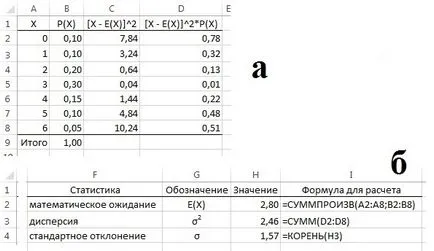
Fig. 2. Calculul succesiva de statistici descriptive variabile discrete aleatoare: (a) datele de intrare și calculele intermediare; (B) calculele finale

Este posibil să se renunțe la calculele intermediare. Pentru a face acest lucru, utilizați formulele matrice (Fig. 3. A se vedea, de asemenea, foaia corespunzătoare atașat Excel-file). Dacă nu ați folosit astfel de formule anterior, recomand să înceapă să citească Excel. Introducerea formula matrice. Interesant este, în unele dintre funcțiile standard Excel sunt deja cu formula matrice, deși puțini. În particular, utilizat anterior SUMPRODUCT = ().

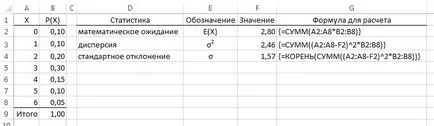
Fig. 3. Calculul statisticii descriptive variabile aleatoare discrete utilizând o serie de formule

Rețineți că pentru puritatea experimentului, este posibil să se facă fără a face referire la o valoare intermediară a E (X) (de exemplu F2 celula de referință în formulele folosite pentru calcularea σ 2 și σ, cm. G3 și G4 celula din Fig. 3). În acest caz, de exemplu, pentru a calcula σ 2 va formula puțin mai greoaie.