Direct în spațiu
Literatura: Colectia de probleme în matematică. Partea 1. Editat de A. V. Efimova, BP Demidovich.
Există forme directe de a scrie ecuația în spațiul:
1) $ \ left \ A_1x + B_1y + C_1z + D_1 = 0 \ quad (P_1) \\ A_2x + B_2y + C_2z + D_2 = 0 \ quad (P_2) \ end \ dreapta. - $ ecuația generală a unei drepte $ L $ în spațiu ca linia de intersecție a două planuri $ P_1 $ și $ P_2 $.
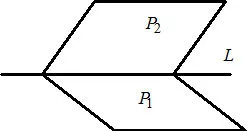
-$ Ecuație Canonical directă $ L $ care trece printr-un punct $ M (x_0, y_0, z_0) $ paralel vector $ \ overline = (m, n, p). $ Vector $ \ overline S $ este vectorul direcția unei drepte $ L. $
3) $ \ frac = \ frac = \ frac - $ ecuația liniei care trece prin cele două puncte $ A (x_1, y_1, z_1) $ și B $ (x_2, y_2, z_2) $.
4) Compararea fiecare dintre părți ale ecuației canonice 2 până la prarametru $ t, se obține o ecuație parametrică a liniei $:
Amplasarea celor două linii în spațiu.
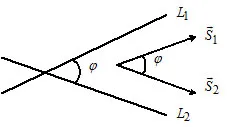
Condiția de paralelism a două linii: Direct $ L_1 $ și $ $ L_2 sunt paralele dacă și numai dacă $ \ overline_1 \ paralel \ overline_2 \ Leftrightarrow $ $ \ frac = \ frac = \ frac $.Starea de perpendicularitate a două linii drepte: $ L_1 \ făptașul L_2 \ Leftrightarrow $ $ \ overline_1 \ făptașul \ overline_2 \ Leftrightarrow $ $ \ cdot + \ cdot + p_1 \ cdot p_2 = 0. $
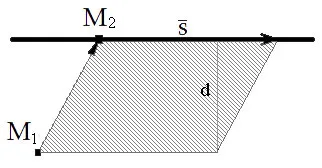
Distanța de la punctul de la linia egală cu lungimea perpendicularei dintr-un punct de pe linia dată.
Lăsați linia $ L $ este dată de $ \ frac = \ frac = \ frac,Astfel $ $ \ overline S = (m, n, p) $ De asemenea, lasa $ M_2 = (x_2, y_2, z_2) -. $ Arbitrara punct aparținând directe $ L. $ Apoi distanța de la $ M_1 = (x_1, y_1 , z_1) $ la linia $ L $ pot fi găsite din formula: $$ d (M_1, L) = \ frac \ overline S] |> $$.
2.198. Scrieți ecuația canonică a liniei care trece prin punctul $ M_0 (2, 0, -3) $ în paralel:
a) $ q vectorul (2, 3, 5); $
e) $ directă x = -2 + t, y = 2t, z = 1 \ fracționare. $
a) utilizarea (2) din ecuația dreptei în spațiu:
$ \ Frac = \ frac = \ frac-$ Ecuație Canonical directă $ L $ care trece printr-un punct $ M (x_0, y_0, z_0) $ paralel vector $ \ overline = (m, n, p). $
Prin ipoteză $ M_0 (2, 0, -3) $ și $ \ overline = q (2, -3,5). $
b) o linie paralelă cu linia dată, trebuie să fie paralelă cu vectorul direcție. vector Direction unei drepte $ \ frac = \ frac = \ frac $ are coordonatele $ \ overline S (5, 2, -1). $ Apoi, găsiți ecuația o linie dreaptă care trece un $ M_0 punctul (2, 0, -3) paralelă cu vectorul $ $ \ overline S (5, 2, 1) $ ca în etapa a):
a) axa OX este vectorul de direcție $ i = (1, 0, 0) $ Astfel, caută o ecuație liniară care trece punct $ M_0 (2, 0, -3) paralelă cu vectorul $ $ i (1, 0, 0) .: $
d) Direct definit ca intersecția a două planuri perpendiculare pe normalele celor două planuri. prin urmare, vectorul de direcție al unei linii drepte
$ \ Stânga \ 3x-y + 2z-7 = 0, \\ x + 3y-2z-3 = 0; \ End \ dreapta. $ Poate fi definit ca produsul transversală a setului de avioane normale.
Pentru avion $ P_1: $ $ 3x-y + 2z-7 $ 0 = coordonatele normale vector are N_1 $ (3, -1, 2); $
pentru plososti $ P_2: $ $ x + 3y-2z-3, $ vector obișnuit are coordonatele $ N_2 (1, 3, -2) $.
Am găsit produsul vectorial:
Astfel, vectorul de direcție al unui $ \ dreapta la stânga \ 3x-y + 2z-7 = 0, \\ x + 3y-2z-3 = 0; \ End \ dreapta. $ Are coordonatele $ \ overline S (-4, 8, 10). $
În continuare trebuie să găsim ecuația o linie dreaptă care trece un $ M_0 punctul (2, 0, -3) paralelă cu vectorul $ $ \ overline S (-4, 8, 10): $
e) Găsiți vectorul direcția unei $ drepte x = -2 + t, y = 2t, z = 1 \ $ Scriem fracționare ecuația acestei linii în formă canonică .:
Prin urmare, vom găsi vectorul de direcție $ \ overline S \ stânga (1, 2, - \ frac \ dreapta) de coordonate $ multiplica vector de direcție cu 2 (pentru a scăpa de fracții): $ \ S_1 overline (2, 4, -1) $ ..
În continuare trebuie să găsim ecuația o linie dreaptă care trece un $ M_0 punctul (2, 0, -3) paralelă cu vectorul $ $ \ overline S (2, 4, 1): $
2.199 (a). Scrieți ecuația liniei care trece prin cele două puncte $ M_1 având în vedere (1, -2, 1) $ și M_2 $ (3, 1, -1). $
Folosind formula (3) în spațiul unei ecuații directe:
$ \ Frac = \ frac = \ frac - $ ecuația liniei care trece prin cele două puncte $ A (x_1, y_1, z_1) $ și B $ (x_2, y_2, z_2) $.
Substituind punctele date:
2.204. Găsiți distanța dintre liniile paralele
Distanța dintre liniile paralele $ L_1 $ și $ L_2 $ este distanța de la un punct arbitrar drept $ L_1 $ directe $ L_2. $ În consecință, poate fi găsită prin formula $$ d (L_1, L_2) = d (M_1, L_2) = \ frac, \ overline S] |>, $$ în cazul în care $ M_1- $ punct arbitrar de pe linia de $ L_1, $ $ M_2 - $ punct arbitrar de pe linia de $ L_2, $ $ \ overline S - $ vector direcția unei drepte $ L_2 $.
Din ecuațiile canonice iau directe M_1 punct $ = (2, -1, 0) \ în L_1, $ $ M_2 = (7, 1, 3) \ în L_2, $ $ \ overline S = (3, 4, 2). $
Ca atare, găsim $ \ overline = (7-2, 1 - (- 1), 3-0) = (5, 2, 3); $
$ [\ Overline, \ overline S] = \ beginijk \\ \\ 523 342 \ end = i (4-12) -j (10-9) + k (20-6) = $ $ = - 8i-j + 14k. $
Pentru a găsi distanța de la $ A $ la linia de L $, $, avem nevoie pentru a alege un punct arbitrar $ M, $ aparținând directe $ L $ și de a găsi un vector de direcție al liniei.
Alegeți un punct de $ $ M. Să coordonatele $ z = 0. $ Substituind această valoare în sistem:
Astfel, $ M = (- 14, - \ frac, 0) $
Noi găsim vectorul de direcție ca produs vectorial al avionului normale definite:
Pentru avion $ P_1: $ $ 2x-2y + z + 3 = 0 $ vector obișnuit are coordonatele N_1 $ (2, -2, 1); $
pentru plososti $ P_2: $ $ 3x + 2y + 2z + 17 = 0, $ vector obișnuit are coordonatele $ N_2 (3, -2, 2) $.
Am găsit produsul vectorial:
Astfel, vectorul de direcție al unui $ \ dreapta la stânga \ 2x-2y + z + 3 = 0, \\ 3x-2y + 2z + 17 = 0 \ end \ dreapta. $
are coordonatele $ \ overline S (-2, -1, 2). $
Acum putem folosi formula $$ d (A, L) = \ frac \ overline S] |.> $$
$ \ Overline = \ stânga (2 - (- 14), 3- \ stânga (- \ frac \ dreapta), - 1-0 \ dreapta) = \ stânga (16, 15 \ frac, -1 \ dreapta) $
$ [\ Overline, \ overline S] = \ beginijk \\ 1615,5-1 \\ - C2-12 \ end = i (31-1) -j (32-2) + k (-16 + 31) = $ $ = 30i-30J + 15k. $
2.212. Scrieți ecuația canonică a unei linii care trece prin M_0 punctul $ (3, -2, -4) $ $ paralel cu planul P: 3x-2y-3Z-7 = 0 și intersectează linia $ $ L: \ frac = \ frac = \ frac . $
Ecuația $ avion P_1, $ care trece prin punctul M_0 $ (3, -2, -4) paralelă cu planul $ $ 3x-2y-3Z-7 = 0: $
$ P :. 3x-2y-3Z-7 = 0 \ rightarrow \ overline N = (3, -2, -3) avionul $ favorizați trece prin punctul M_0 $ (3, -2, -4) perpendicular vector $ $ \ overline N (3, -2, -3). $
$ P_1: 3x-9-2y-4-3z-12 = 0 \ rightarrow $
În continuare, găsiți punctul de intersecție al $ $ P_1 plan și $ L $ linie dreaptă vom scrie o ecuație $ L $ liniar în formă parametrice:
Apoi, înlocuind valoarea $ x, y $ și $ z, $ exprimate prin $ t $ ecuație $ avion în P_1, $, și din care rezultă ecuația vyrazm $ t: $
Substituind găsit $ t $ valoare poate fi setată într-o linie dreaptă ecuație L $, $ găsi coordonatele punctelor de intersecție:
Astfel, $ directă L $ și $ P_1 $ plan se intersectează într-un punct $ M_1 (8, -8, 5). $
Acum vom scrie ecuația liniei care trece prin punctele M_0 $ $ Și M_1 $ (8, -8, 5) $ (3, -2, -4.) - aceasta va fi linia dorită. Noi folosim formula (3) $ \ frac = \ frac = \ frac: $
b) Scrieți ecuația liniei care trece prin cele două puncte $ M_1 Având în vedere (3, -1, 0) și $ $ M_2 (1, 0, -3). $
2.206. Demonstrati ca liniile $ L_1: \ left \ 2x + 2y-z-10 = 0, \\ end xyz-22 = 0, \ \ dreapta si $ L_2: .. \ Frac = \ frac = \ frac $ paralele și găsi distanța $ \ Rho (L_1, L_2) $
2.207. Creați ecuație linie dreaptă care trece prin $ x-3y + 2Z puncte de intersecție ale planului 0 + 1 = $ drept $ \ frac = \ frac = \ frac $ și $ \ frac = \ frac = \ frac. $
2.211. Scrieți ecuația liniei care trece prin punctul $ M_0 (7, 1, 0) plan paralel $ $ 2x + 3y-z-15 = $ 0 și intersectând linia $ \ frac = \ frac = \ frac. $