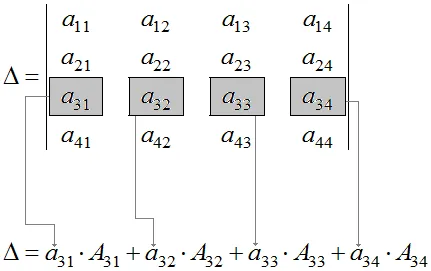
Descompunerea determinant pe rând (coloană)

Determinant pentru al patrulea și mai înalte ordine ale altor metode de calcul utilizate în mod obișnuit decât utilizarea formulelor gata pentru calcularea determinanților doua și a treia comenzi. O metodă de calcul factori determinanți de ordin superior - utilizarea anchetei teoremei Laplace (teorema în sine poate fi văzut, de exemplu, în cartea AG Kurosh „Cursul superior Algebra“). Acest lucru permite, în consecință determinant descompuși prin elementele unui rând sau coloană. In acest calcul al determinantului de ordinul n-lea reduce la calculul determinanților n (n-1), comanda -lea. De aceea, această transformare se numește ordine descrescătoare determinant. De exemplu, calculul determinant al patrulea ordinul este redusă la găsirea celor patru determinanți ai treilea ordin.

Să presupunem că avem o matrice pătratică de ordinul n-lea, de exemplu, $ A = \ stânga (\ începe a_ a_ \ ldots a_ \\ a_ a_ \ ldots a_ \\ \ ldots \ ldots \ ldots \ Ldots \\ a_ a_ \ ldots a_ \\ \ end \ dreapta) $. Se calculează determinantul acestei matrici este posibil, extinderea acesteia pe linie sau coloana.

Am repara o linie, al căror număr este egal cu $ i $. Apoi determinantul $ A_ $ poate fi extins în rândul selectat i-lea, folosind următoarea formulă:

$ A_ $ reprezintă cofactor al elementului $ a_ $. Pentru mai multe informații despre acest concept am recomanda sa se uite si de tema cofactor minorilor. Record $ a_ $ este un element al matricei sau determinant poziționat la intersecția coloanei j-a rândul i-lea. Tema Matrix poate căuta mai multe informații. Tipuri de matrici. termeni de bază.

Să presupunem că vrem să găsim suma de $ 1 ^ 2 + 2 ^ 2 + 3 ^ 2 + 4 ^ 2 + 5 ^ 2 $. Ce teză poate fi caracterizat printr-un record de $ 1 ^ 2 + 2 ^ 2 + 3 ^ 2 + 4 ^ 2 + 5 ^ 2 $? Putem spune acest lucru: este suma unității în pătrat, pătrat de două, în piața treiari, cele patru cinciari pătrați și pătrat. Și tu poți spune că scurt: este suma pătratelor numere întregi de la 1 la 5. Pentru a exprima valoarea unui scurt și servește ca o înregistrare folosind litere $ \ sum $ (este greacă litera „sigma“).

În loc de $ 1 ^ 2 + 2 ^ 2 + 3 ^ 2 + 4 ^ 2 + 5 ^ 2 $, putem utiliza următoarea intrare: $ \ sum \ limits_ ^ i ^ 2 $. Scrisoare $ i $ este numit indicele de însumare. iar numerele 1 (valoarea inițială a $ i $) și 5 ($ i $ finală), numit mai mici și limitele superioare ale însumării, respectiv.

Descifra un record de $ \ sum \ limits_ ^ i ^ 2 $ în detaliu. Dacă $ i = 1 $, atunci $ i ^ 2 = 1 ^ 2 $, astfel încât primul termen al acestei sume este numărul de $ 1 ^ 2 $:

În continuare întreg după ce unitatea - două, astfel încât înlocuind $ i = 2 $, obținem: $ i ^ 2 = 2 ^ 2 $. Suma va fi acum după cum urmează:

După următorul număr de două - trei, astfel încât înlocuind $ i = $ 3 va fi: $ i = 2 ^ 3 ^ 2 $. Iar suma devine:

Rămâne să înlocuiască doar două numere: 4 și 5. Dacă înlocuim $ i = 4 $, de $ i ^ 2 = 4 ^ 2 $, iar dacă vom înlocui $ i = 5 $, atunci $ i ^ 2 = 5 ^ 2 $. Valorile $ i $ atins limitele superioare ale însumării, astfel încât termenul este de 5 $ ^ 2 $ să fie ultima. Deci, suma finală este acum după cum urmează:

Această sumă poate fi calculată și, numărul bătături pliat: $ \ sum \ limits_ ^ i ^ 2 = $ 55 de ani.

Pentru practica, încercați să înregistreze și să calculeze suma dintre următoarele: $ \ sum \ limite _ ^ (5k + 2) $. Indicele aici ınsumarea - scrisoarea $ k $, limita inferioară a însumare este egal cu 3, iar limita superioară a însumare este egală cu 8.

Un analog cu formula (1) există și pentru coloanele. Formula pentru extinderea determinantul coloanei j-a este următoarea:

Regulile exprimate prin formulele (1) și (2) poate fi formulată după cum urmează: determinant este egal cu suma produselor unor elemente ale unui rând sau o coloană de pe cofactori acestor elemente. Pentru claritate, considerăm determinantul al patrulea ordin, înregistrate într-un mod general:

Am ales o coloană de arbitrar în determinant. Să luăm, de exemplu, sub numărul 4. Coloana a scrie formula pentru descompunerea determinantului coloanei selectate patra:

În mod similar, prin alegerea, de exemplu, al treilea rând, se obține extinderea acestei linii:

Se calculează determinantul matricei $ A = \ left (\ begin 5 -4 3 \\ 7 2 -1 \\ 9 0 4 \ end \ dreapta) $, folosind extinderea primului rând și a doua coloana.

Trebuie să calculeze determinant al treilea ordin de $ \ Delta A = \ left | \ Începe 5 -4 3 \\ 7 2 -1 \\ 9 0 4 \ end \ dreapta | $. Pentru a-l extinde, în primul rând, trebuie să utilizați formula (1). Scriem această expansiune în termeni generali:

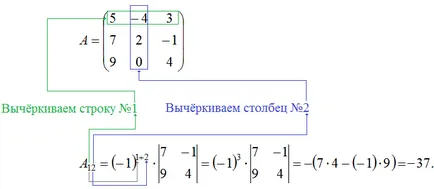
Pentru noastre matrice $ a_ = 5 $, $ a _ = - 4 $, $ a_ = 3 $. Pentru a calcula cofactori $ A_ $, $ A_ $, $ $ A_ sa folosim formula №1 de fire dedicate determinanții doua și a treia comenzi. Astfel, cofactori necesare ale acestora sunt:

\ începe A _ = (- 1) ^ 2 \ cdot \ left | \ Începe 2 -1 \\ 0 4 \ end \ dreapta | = 2 \ cdot 4 - (- 1) \ cdot 0 = 8; \\ A _ = (- 1) ^ 3 \ cdot \ left | \ Începe 7 -1 \\ 9 4 \ end \ dreapta | = - (7 \ cdot 4 - (- 1) \ cdot 9) = - 37; \\ A _ = (- 1) ^ 4 \ cdot \ left | \ Începe 7 2 \\ 9 0 \ end \ dreapta | = 7 \ cdot 0-2 \ cdot 9 = -18. \ end

Cum găsim cofactori? Afișați \ ascunde

Pentru mai multe informații despre acest concept am recomanda sa se uite si de tema cofactor minorilor. Scurt sunt exprimate în figura de mai jos:

Substituind valorile obținute înregistrate în formula de mai sus, obținem:

După cum puteți vedea, găsirea determinantul al treilea proces comanda am redus la calcularea valorilor trei dintre determinanții de ordinul al doilea. Cu alte cuvinte, am redus ordinea de start determinant.

De obicei, în astfel de cazuri, vopseaua obișnuită nu este o soluție în detaliu, găsind separat cofactori, și numai apoi înlocuind-le în formulă pentru a calcula determinant. Cel mai adesea, doar ține un registru cu formula generală - până când se primește un răspuns. Acesta este modul în care vom expune determinantul din a doua coloană.

Deci, vom proceda la extinderea determinantul a doua coloană. Calculul auxiliar nu va produce - trebuie doar să continue cu formula pentru a obține un răspuns. De notat că, în a doua coloană a unui element este zero, adică $ A_ = 0 $. Acest lucru sugerează că termenul de $ a_ \ cdot A_ = 0 \ cdot A_ = 0 $. Folosind ecuația (2), pentru a doua coloană de expansiune, obținem:

$$ \ Delta A = a_ \ cdot A_ + a_ \ cdot A_ + a_ \ cdot A _ = - 4 \ cdot (-1) \ cdot \ din stânga | \ Începe 7 -1 \\ 9 4 \ end \ dreapta | 2 \ cdot \ left | \ Începe 5 3 \\ 9 4 \ end \ dreapta | = 4 \ cdot 37 + 2 \ cdot (-7) = 134. $$

Răspunsul este primit. Desigur, rezultatul unei expansiuni în a doua coloană a coincis cu rezultatul primei linii de expansiune, pentru că ne-am pus în același determinant. Rețineți că extinderea în a doua coloană calculele am efectuat mai mici, ca un element al a doua coloană este egală cu zero. Este din cauza acestor motive pentru degradarea încerca să aleagă rândul sau coloana care conțin mai multe zerouri.

Răspuns. $ \ Delta A = $ 134.

Se calculează determinantul $ matricea A = \ left (\ începe -1 3 2 -3 \\ 4 -2 5 1 \\ -5 0 -4 0 \\ 9 7 8 -7 \ end \ dreapta) $, folosind extinderea rândul sau coloana selectată.

Pentru descompunerea este cea mai avantajoasă pentru a selecta rândul sau coloana care conține un total de zerouri. Firește, în acest caz, este logic să se stabilească pe al treilea rând, deoarece acesta cuprinde două elemente, egale cu zero. Folosind formula (1). vom scrie extinderea determinant al treilea rând:

Deoarece $ a _ = - $ 5, $ a_ = 0 $, $ a _ = - 4 $, $ a_ = $ 0, formula de mai sus vor fi înregistrate după cum urmează:

$$ \ Delta A = -5 \ cdot A_-4 \ cdot A_. $$

Să ne întoarcem la cofactori de $ A_ $ și $ A_ $. Pentru a calcula le va folosi formula №2 firelor determinanți ai doilea și al treilea comenzi dedicate (în aceeași secțiune există exemple detaliate de aplicare a acestei formule).

\ începe A _ = (- 1) ^ 4 \ cdot \ left | \ Begin 3 2 -3 -2 \\ 5 1 \\ 7 8 -7 \ end \ dreapta | = 10; \\ A _ = (- 1) ^ 6 \ cdot \ left | \ Begin -1 3 -3 \\ 4 -2 1 \\ 9 7 -7 \ end \ dreapta | = -34. \ end

Înlocuind aceste date în formula pentru determinantul, avem:

$$ \ Delta A = -5 \ cdot A_-4 \ cdot A _ = - 5 \ cdot 10-4 \ cdot (-34) = 86. $$

În principiu, toată soluția poate fi scrisă într-o singură linie. Dacă ți-e dor toate explicațiile și calculele intermediare, înregistrarea deciziei va fi după cum urmează:

$$ \ Delta A = a_ \ cdot A_ + a_ \ cdot A_ + a_ \ cdot A_ + a_ \ cdot A _ = \\ = -5 \ cdot (-1) ^ 4 \ cdot \ din stânga | \ Begin 3 2 -3 -2 \\ 5 1 \\ 7 8 -7 \ end \ dreapta | -4 \ cdot (-1) ^ 6 \ cdot \ din stânga | \ Begin -1 3 -3 \\ 4 -2 1 \\ 9 7 -7 \ end \ dreapta | = -5 \ cdot 10-4 \ cdot (-34) = 86. $$

Răspuns. $ \ Delta A = $ 86.