derivați de soluție de

Pentru a înțelege definiția unui derivat, luați în considerare următorul grafic al funcției.

Fig.1. Un exemplu de funcție și derivatul său.

Privind la imaginea pe care se poate vedea locurile în care funcția este în creștere rapidă, și în cazul în care scade. De exemplu, din punctul b la punctul de un grafic se ridică mai rapid decât din punctul b la punctul c.

Dacă mutați punctul la graficul funcției la noul sistem de coordonate, astfel încât să crească punctul situat deasupra axei x, iar punctul de a coborî sub axa x (după scală) și conectați puncte, veți obține un nou calendar pentru noile funcții (graficul de jos în Fig. 1 ). Această funcție este derivata funcției primare. Acest grafic nu este nimic, ca indicator al ratei de schimbare a funcțiilor. Cu alte cuvinte, derivatul - funcția de schimbare a vitezei. În practică, derivații sunt folosite pentru a determina rata de schimbare a unor procese: fizice, chimice, economice, etc.

In limbaj mai complex, derivatul - este limita spre care raportul dintre increment la incrementarea x y. În general, funcția derivat arată și este definit după cum urmează:

Procesul de calculare a funcției derivat se numește prin diferențierea.

Funcții găsit în practică foarte mulți, dar există o funcție simplă (de bază), cum ar fi, F (x) = sinx, F (x) = C (unde C este o constantă), F (x) = LNX etc. Pentru aceste funcții elementare deja definite derivați, și suficient de ei pentru a învăța pe de rost. derivați simple funcții (de bază) sunt prezentate în tabelul de mai jos.

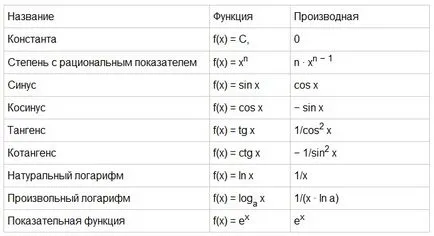
Fig.2. Tabelul simple derivate funcții (de bază).

derivați de soluție. în termeni simpli, este de a transforma o funcție la alta, urmând anumite reguli (excepția este funcția exponențială F (x) = e ^ x, care nu se schimba).

Să considerăm un exemplu. Este necesar să se găsească derivata funcției F (x) = x ^ 3 + 3x ^ 2 - 72x + 90
Pentru a rezolva derivatul este suficient pentru a utiliza tabelul de derivați de funcții simple (elementare). În conformitate cu datele din tabelul obține derivatul:
F '(x) = (x ^ 3 + 3x ^ 2 - 72x + 90)' = 3x ^ 2 + 6x-72

Soluția derivatului complex

În practică, decizia a derivaților de funcții complexe, trebuie să se confrunte mai des decât simpla.

O regulă pentru determinarea derivata unei funcții compozit după cum urmează:
(A (b)) '= a' (b) * b“, în cazul în care un extern funcție, b-internă funcție.

Este necesar să se găsească derivata funcției F (x) = sin (3x-5)

Găsiți derivatul acestei funcții, utilizați tabelul de funcții simple (elementare) nu vor funcționa ca un păcat este o expresie întreg, adică Funcția constă în două funcții a = sin (x) (funcția externă) și b = 3x 5 (funcție internă).

Noi folosim definiția regula derivatului unei funcții compozit și se obține:
F '(x) = (sin (3x-5))' = cos (3x-5) * (3x-5) „= 3cos (3x-5).

În cazul în care materialul a fost util otblagorit, site-ul nostru puteți de a face o donație.
Orice cantitate de dezvoltare a proiectului, puteți dona pe această pagină.